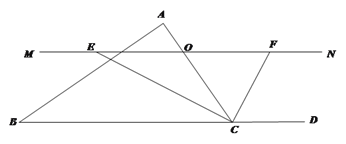
【题目】已知△ABC中,点O是边AC上的一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF.
(2)试确定点O在边AC上的位置,使四边形AECF是矩形,并加以证明.
(3)在(2)的条件下,且△ABC满足 ____________时,矩形AECF是正方形.
参考答案:
【答案】∠BAC=90°
【解析】分析:(1)由平行线的性质和角平分线的性质,推出∠ECB=∠CEO,∠GCF=∠CFO,∠ECB=∠ECO,∠GCF=∠OCF,通过等量代换即可推出∠CEO=∠ECO,∠CFO=∠OCF,便可确定OC=OE,OC=OF,可得OE=OF;
(2)当O点运动到AC的中点时,四边形AECF为矩形,根据矩形的判定定理(对角线相等且互相平分的四边形为矩形),结合(1)所推出的结论,即可推出OA=OC=OE=OF,求出AC=EF后,即可确定四边形AECF为矩形;
(3)当△ABC是直角三角形时,四边形AECF是正方形,根据(2)所推出的结论,由AC⊥BC,MN∥BC,确定AC⊥EF,即可推出结论.
详解:(1)∵CE是∠ACB的平分线,∴∠ACE=∠BCE.
∵MN∥BC,∴∠FEC=∠BCE,∴∠ACE=∠FEC,∴OE=OC,
同理可证OF=OC,
∴OE=OF;
(2)当点O运动到AC中点时,四边形AECF是矩形.
∵OA=OC,OE=OF,∴四边形AECF平行四边形.
∵OE=OC,∴OA=OC=OE=OF,∴AC=EF,
∴平行四边形AECF是矩形;
(3)当点O运动到AC的中点,且△ABC满足∠ACB=90°时,四边形AECF是正方形.理由如下:
∵当点O运动到AC的中点时,AO=CO.
又∵EO=FO,∴四边形AECF是平行四边形.
∵FO=CO,∴AO=CO=EO=FO,∴AO+CO=EO+FO,即AC=EF,∴四边形AECF是矩形.
∵MN∥BC,当∠ACB=90°,则∠AOF=∠COE=∠COF=∠AOE=90°,∴AC⊥EF,∴四边形AECF是正方形;
故答案为:∠ACB=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C
与x轴的负半轴交于点A,与y轴交于点B,连结AB.点C  在抛物线上,直线AC与y轴交于点D.
在抛物线上,直线AC与y轴交于点D.
(1)求c的值及直线AC的函数表达式;
(2)点P在x轴的正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.
①求证:△APM∽△AON;
②设点M的横坐标为m , 求AN的长(用含m的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连接对角线相等的四边形的四边中点,所得的四边形一定是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为做好食堂的服务工作,某学校食堂对学生最喜爱的菜肴进行了抽样调查,下面试根据收集的数据绘制的统计图(不完整):
(1)参加抽样调查的学生数是______人,扇形统计图中“大排”部分的圆心角是______°;
(2)把条形统计图补充完整;
(3)若全校有3000名学生,请你根据以上数据估计最喜爱“烤肠”的学生人数.


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知有理数a、b、c在数轴上对应的点如图所示,则下列结论正确的是( )
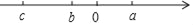
A. c+b>a+b B. cb<ab C. ﹣c+a>﹣b+a D. ac>ab
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在下列表格中填上相应的值
x
…
-6
-4
-3
-2
-1
1
2
3
4
6
…
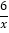
…
-1
-2
3
1
…

(2)若将上表中的变量
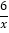 用y来代替(即有
用y来代替(即有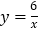 ),请以表中的
),请以表中的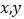 的值为点的坐标, 在下方的平面直角坐标系描出相应的点,并用平滑曲线顺次连接各点
的值为点的坐标, 在下方的平面直角坐标系描出相应的点,并用平滑曲线顺次连接各点(3)在(2)的条件下,可将y看作是x的函数 ,请你结合你所画的图像,写出该函数图像的两个性质 :__________________________________________________.
(4)结合图像,借助之前所学的函数知识,直接写出不等式
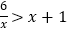 的解集: ____________
的解集: ____________ -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)方法回顾:在学习三角形中位线时,为了探索三角形中位线的性质,思路如下:
第一步添加辅助线:如图1,在
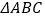 中,延长
中,延长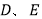 (
(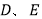 分别是
分别是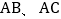 的中点)到点
的中点)到点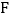 ,使得
,使得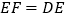 ,连接
,连接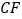 ;
;第二步证明
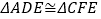 ,再证四边形
,再证四边形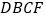 是平行四边形,从而得出三角形中位线的性质结论:____________________________________(请用DE与BC表示)
是平行四边形,从而得出三角形中位线的性质结论:____________________________________(请用DE与BC表示)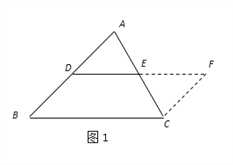
(2)问题解决:如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.

(3)拓展研究:如图3,在四边形ABCD中,∠A=105°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=
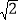 ,DF=2,∠GEF=90°,求GF的长.
,DF=2,∠GEF=90°,求GF的长.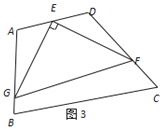
相关试题

