【题目】(1)方法回顾:在学习三角形中位线时,为了探索三角形中位线的性质,思路如下:
第一步添加辅助线:如图1,在![]() 中,延长
中,延长![]() (
(![]() 分别是
分别是![]() 的中点)到点
的中点)到点![]() ,使得
,使得![]() ,连接
,连接![]() ;
;
第二步证明![]() ,再证四边形
,再证四边形![]() 是平行四边形,从而得出三角形中位线的性质结论:____________________________________(请用DE与BC表示)
是平行四边形,从而得出三角形中位线的性质结论:____________________________________(请用DE与BC表示)
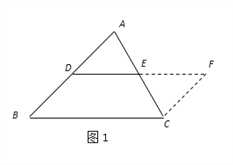
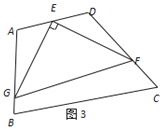
(2)问题解决:如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.

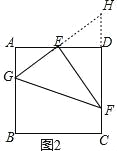
(3)拓展研究:如图3,在四边形ABCD中,∠A=105°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=![]() ,DF=2,∠GEF=90°,求GF的长.
,DF=2,∠GEF=90°,求GF的长.
参考答案:
【答案】DE∥BC,DE=![]() BC.
BC.
【解析】分析:(1)直接得出结论即可;
(2)延长GE、FD交于点H,可证得△AEG≌△DEH,结合条件可证明EF垂直平分GH,可得GF=FH,可求得GF的长;
(3)过点D作AB的平行线交GE的延长线于点H,过H作CD的垂线,垂足为P,连接HF,可证明△AEG≌△DEH,结合条件可得到△HPD为等腰直角三角形,可求得PF的长.在Rt△HFP中,可求得HF,则可求得GF的长.
详解:(1)DE∥BC,DE=![]() BC;
BC;
(2)如图2,延长GE、FD交于点H,

∵E为AD中点,
∴EA=ED,且∠A=∠EDH=90°,
在△AEG和△DEH中,
∵∠A=∠EDH,EA=ED,∠AEG=∠HED,
∴△AEG≌△DEH(ASA),
∴AG=HD=2,EG=EH.
∵∠GEF=90°,
∴EF垂直平分GH,
∴GF=HF=DH+DF=2+3=5;
(3)如图3,过点D作AB的平行线交GE的延长线于点H,过H作CD的垂线,垂足为P,连接HF,
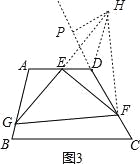
同(1)可知△AEG≌△DEH,GF=HF,
∴∠A=∠HDE=105°,AG=HD=3.
∵∠ADC=120°,
∴∠HDF=360°﹣105°﹣120°=135°,
∴∠HDP=45°,
∴△PDH为等腰直角三角形,
∴PD=PH=1.
∵DF=2,
∴PF=PD+DF=1+2=3,
∴GF=HF=![]() .
.
-
科目: 来源: 题型:
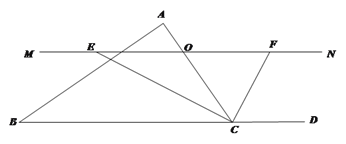
查看答案和解析>>【题目】已知△ABC中,点O是边AC上的一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF.
(2)试确定点O在边AC上的位置,使四边形AECF是矩形,并加以证明.
(3)在(2)的条件下,且△ABC满足 ____________时,矩形AECF是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知有理数a、b、c在数轴上对应的点如图所示,则下列结论正确的是( )
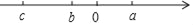
A. c+b>a+b B. cb<ab C. ﹣c+a>﹣b+a D. ac>ab
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在下列表格中填上相应的值
x
…
-6
-4
-3
-2
-1
1
2
3
4
6
…
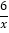
…
-1
-2
3
1
…

(2)若将上表中的变量
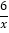 用y来代替(即有
用y来代替(即有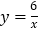 ),请以表中的
),请以表中的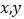 的值为点的坐标, 在下方的平面直角坐标系描出相应的点,并用平滑曲线顺次连接各点
的值为点的坐标, 在下方的平面直角坐标系描出相应的点,并用平滑曲线顺次连接各点(3)在(2)的条件下,可将y看作是x的函数 ,请你结合你所画的图像,写出该函数图像的两个性质 :__________________________________________________.
(4)结合图像,借助之前所学的函数知识,直接写出不等式
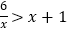 的解集: ____________
的解集: ____________ -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根,比如对于方程
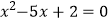 ,操作步骤是:
,操作步骤是:
第一步:根据方程系数特征,确定一对固定点A(0,1),B(5,2);
第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点A,另一条直角边恒过点B;
第三步:在移动过程中,当三角板的直角顶点落在x轴上点C处时,点C 的横坐标m即为该方程的一个实数根(如图1)
第四步:调整三角板直角顶点的位置,当它落在x轴上另一点D处时,点D 的横坐标为n即为该方程的另一个实数根。
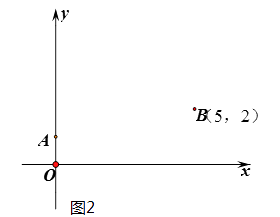
(1)在图2 中,按照“第四步“的操作方法作出点D(请保留作出点D时直角三角板两条直角边的痕迹)
(2)结合图1,请证明“第三步”操作得到的m就是方程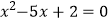 的一个实数根;
的一个实数根;
(3)上述操作的关键是确定两个固定点的位置,若要以此方法找到一元二次方程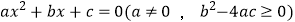 的实数根,请你直接写出一对固定点的坐标;
的实数根,请你直接写出一对固定点的坐标;
(4)实际上,(3)中的固定点有无数对,一般地,当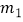 ,
, 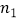 ,
, 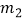 ,
, 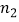 与a,b,c之间满足怎样的关系时,点P(
与a,b,c之间满足怎样的关系时,点P( 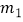 ,
, 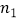 ),Q(
),Q( 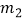 ,
, 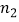 )就是符合要求的一对固定点?
)就是符合要求的一对固定点? -
科目: 来源: 题型:
查看答案和解析>>【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的液体,并用流量、速度、密度三个概念描述车流的基本特征。其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度;密度(辆/千米)指通过道路指定断面单位长度内的车辆数,为配合大数据治堵行动,测得某路段流量q与速度v之间的部分数据如下表:
速度v(千米/小时)
…
5
10
20
32
40
48
…
流量q(辆/小时)
…
550
1000
1600
1792
1600
1152
…
(1)根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是(只需填上正确答案的序号)① ②
② 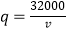 ③
③ 
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速为多少时,流量达到最大?最大流量是多少?
(3)已知q,v,k满足 ,请结合(1)中选取的函数关系式继续解决下列问题:
,请结合(1)中选取的函数关系式继续解决下列问题:
①市交通运行监控平台显示,当 时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:
(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形;
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形;
(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.
(请将三个小题依次作答在图1、图2、图3中,均只需画出符合条件的一种情形)

相关试题

