搜索
【题目】顺次连接对角线相等的四边形的四边中点，所得的四边形一定是____________.
参考答案：
【答案】菱形
【解析】分析：作出图形，根据三角形的中位线平行于第三边并且等于第三边的一半可得EF=
AC，GH=AC，HE=BD，FG=BD，再根据四边形的对角线相等可可知AC=BD，从而得到EF=FG=GH=HE，再根据四条边都相等的四边形是菱形即可得解．
详解：如图，E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点，根据三角形的中位线定理，EF=AC，GH=AC，HE=BD，FG=BD，连接AC、BD．
∵四边形ABCD的对角线相等，∴AC=BD，所以，EF=FG=GH=HE，所以，四边形EFGH是菱形．
故答案为：菱形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，过抛物线y=
x2﹣2x上一点A作x轴的平行线，交抛物线于另一点B，交y轴于点C，已知点A的横坐标为﹣2．
（1）求抛物线的对称轴和点B的坐标；
（2）在AB上任取一点P，连结OP，作点C关于直线OP的对称点D；
①连结BD，求BD的最小值；
②当点D落在抛物线的对称轴上，且在x轴上方时，求直线PD的函数表达式． -
科目： 来源： 题型：
查看答案和解析>>【题目】湖州素有鱼米之乡之称，某水产养殖大户为了更好地发挥技术优势，一次性收购了
淡水鱼，计划养殖一段时间后再出售．已知每天放养的费用相同，放养 
天的总成本为 
万元；放养 
天的总成本为 
万元（总成本=放养总费用+收购成本）．
（1）设每天的放养费用是
万元，收购成本为 
万元，求 和 的值；
（2）设这批淡水鱼放养
天后的质量为 
（ ），销售单价为 
元/ ．根据以往经验可知： 与 的函数关系为 
； 与 的函数关系如图所示．
①分别求出当
和 
时， 与 的函数关系式；
②设将这批淡水鱼放养 天后一次性出售所得利润为 
元，求当 为何值时， 最大？并求出最大值．（利润=销售总额-总成本） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线
与x轴的负半轴交于点A，与y轴交于点B，连结AB．点C 
在抛物线上，直线AC与y轴交于点D．
（1）求c的值及直线AC的函数表达式；
（2）点P在x轴的正半轴上，点Q在y轴正半轴上，连结PQ与直线AC交于点M，连结MO并延长交AB于点N，若M为PQ的中点．
①求证：△APM∽△AON；
②设点M的横坐标为m ， 求AN的长（用含m的代数式表示）． -
科目： 来源： 题型：
查看答案和解析>>【题目】为做好食堂的服务工作，某学校食堂对学生最喜爱的菜肴进行了抽样调查，下面试根据收集的数据绘制的统计图（不完整）：
（1）参加抽样调查的学生数是______人，扇形统计图中“大排”部分的圆心角是______°；
（2）把条形统计图补充完整；
（3）若全校有3000名学生，请你根据以上数据估计最喜爱“烤肠”的学生人数．
-
科目： 来源： 题型：
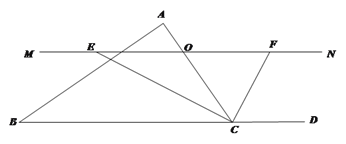
查看答案和解析>>【题目】已知△ABC中，点O是边AC上的一个动点，过O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．
（1）求证：OE=OF．
（2）试确定点O在边AC上的位置，使四边形AECF是矩形，并加以证明．
（3）在（2）的条件下，且△ABC满足 ____________时，矩形AECF是正方形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知有理数a、b、c在数轴上对应的点如图所示，则下列结论正确的是（ ）
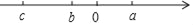
A. c+b＞a+b B. cb＜ab C. ﹣c+a＞﹣b+a D. ac＞ab
相关试题
