【题目】已知A,B在数轴上表示的数分别是m,n.
(1)填写下表:

(2)若A,B两点间的距离为d,写出d与m,n之间的数量关系.
(3)在数轴上标出所有符合条件的整数点P,使它到5和-5的距离之和为10,并求出所有这些整数的和.
参考答案:
【答案】(1)2,5,10,2,12,0;(2)d=|m-n|;(3)在数轴上标出略,整数点P表示的数可以是5,-5,4,-4,3,-3,2,-2,1,-1,0,它们的
和是0.
【解析】
根据在数轴求距离的方法,让右边的点表示的数减去左边的点的表示的数,依次计算可得答案.
数轴上两点间的距离d等于表示两点数之差的绝对值,即d=|m-n|.
设P点为x,根据(2)得出的结论列出含绝对值的一元一次方程,利用绝对值的代数意义化简即可求出x的值.
解:(1)从左到右依次填2,5,10,2,12,0.
(2)d=|m-n|.
(3) 5,-5,4,-4,3,-3,2,-2,1,-1,0,它们的 和是0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣3)+7+(﹣6)+(﹣7)
(2)(-20)+(+3)-(-5)-(+7)
(3)(﹣3.5)×(﹣2)÷(-
 )÷(﹣5)
)÷(﹣5)(4)﹣14+16÷(﹣2)3×|﹣3﹣1|
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括O、B),做MN⊥DM,垂足为M,交∠CBE的平分线于点N.
(1)求点C的坐标;
(2)求证:MD=MN;
(3)如图(2),连接DN交BC于F,连接FM,探究线段MF、CF、OM之间有什么数量关系?并证明你的结论.
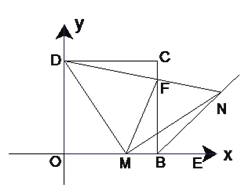
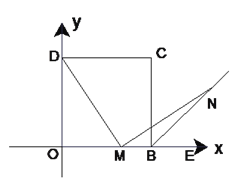
图(1) 图(2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
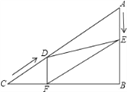
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
-
科目: 来源: 题型:
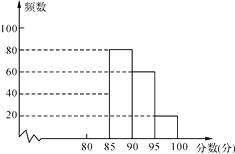
查看答案和解析>>【题目】某校组织了一次G20知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:
分数段
频数
频率
80≤x<85
a
0.2
85≤x<90
80
b
90≤x<95
60
c
95≤x<100
20
0.1
(1)求出表中a,b,c的数值,并补全频数分布直方图;
(2)获奖成绩的中位数落在哪个分数段?
(3)估算全体获奖同学成绩的平均分. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知图所示的计算程序.

根据计算程序回答下列问题:
(1)填写表内空格:
输入x
3
2
-2

…
输出答案
0
…
(2)你发现的规律是 .
(3)用简要过程说明你发现的规律的正确性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2018次运动后,动点P的坐标是_____________.

相关试题

