【题目】如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD。

(1)求证:DE是⊙O的切线;
(2)若tan∠ABD=2,CE=1,求⊙O的半径。
参考答案:
【答案】(1)证明见解析;
(2)b=3或b=![]()
【解析】分析:(1)连接OD,欲证明DE是 O的切线,只要证明OD⊥DE即可.
(2)利用相似三角形的判定和性质求出AB,利用勾股定理求出BD,进而解答即可.
本题解析:
(1)证明:连接OD。

∵OA=OD,∴∠BAD=∠ODA。∵AD平分∠BAC,∴∠BAD=∠DAC。
∴∠ODA=∠DAC。∴OD∥AE。∵DE⊥AE,∴OD⊥DE,∴DE是⊙O的切线.
(2)解:连接CD,连接DO并延长交⊙O于点F。

∵AB是⊙O直径,∴∠ADB=90°。∴∠ADB=∠E。
又∵∠BAD=∠DAC,∴△ABD∽△ADE。
∵DF是⊙O直径,∴∠FCD=90°,∴∠F=∠DAE,
∴∠F+∠FDC=90°,∠CDE+∠FDC=90°,∴∠F=∠CDE=∠DAE,
∴△DCE∽△ADE,∴∠ABD=∠DCE。根据tan∠ABD=2,∴tan∠DCE=2。
在RT△DCE中,CE=1,∴DE=2。
在RT△ADE中,同理可得AE=4,由勾股定理可知AD=2![]() 。
。
在RT△ABD中,同理可得BD=![]() ,由勾股定理可知AB=5。
,由勾股定理可知AB=5。
所以⊙O的半径为2.5。
-
科目: 来源: 题型:
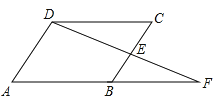
查看答案和解析>>【题目】如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于F点,CD∥AF,请你添加一个条件:使四边形ABCD是平行四边形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果把Rt△ABC的各边长都扩大到原来的n倍,那么锐角A的四个三角比值( )
A.都缩小到原来的n倍B.都扩大到原来的n倍;
C.都没有变化D.不同三角比的变化不一致.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:直线l与直线l外一点A。求作:过点A作直线l的平行线。

小明的作法如下:
如图,

①在直线l上任取两点B,C;
②以点A为圆心,线段BC的长为半径作圆弧;以点C为圆心,线段AB的长为半径作圆弧;两圆弧(与点A在l同侧)的交点为D;
③过点A,D作直线。所以直线AD即为所求。
老师说:“小明的作法正确。”
该作图的依据是_____________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A.经过平面内任意三点可作一个圆
B.相等的圆心角所对的弧一定相等
C.相交两圆的公共弦一定垂直于两圆的连心线
D.内切两圆的圆心距等于两圆的半径的和
-
科目: 来源: 题型:
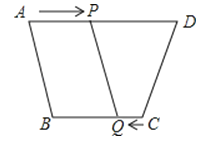
查看答案和解析>>【题目】如图所示,在四边形ABCD中,AD∥CB,且AD>BC,BC=6cm,动点P,Q分别从A,C同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C向B运动,则 秒后四边形ABQP为平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:6x2﹣3x= .
相关试题

