【题目】已知函数y=kx+b的图象与x轴、y轴分别交于点A(12,0),与函数y=x的图象交于点E,点E的横坐标为3.
(1)求函数y=kx+b的表达式;
(2)在x轴上有一点F(a,0),过点F作x轴的垂线,分别交函数y=kx+b的图象和函数y=x的图象于点C,D,若四边形OBDC是平行四边形,求a的值.

参考答案:
【答案】(1)y=﹣![]() x+4;(2)a的值为6.
x+4;(2)a的值为6.
【解析】
(1)将x=3代入y=x中求出y值,即得出点E的坐标,结合点A、E的坐标,利用待定系数法即可求出直线AB的解析式;
(2)由点F的坐标可表示出点C、D的坐标,由此即可得出线段CD的长度,根据平行四边形的判定定理即可得出CD=OB,即得出关于a的方程,解方程即可得出结论.
解:(1)把x=3代入y=x,得y=3,
∴E(3,3),
把A(12,0)、E(3,3)代入y=kx+b中,
得:![]() ,
,
解得: ,
,
∴直线AB的解析式为y=﹣![]() x+4.
x+4.
(2)由题意可知,C、D的横坐标为a,
∴C(a,﹣![]() a+4),D(a,a),
a+4),D(a,a),
∴CD=|a﹣(﹣![]() a+4)|=|
a+4)|=|![]() a﹣4|.
a﹣4|.
若四边形OBDC是平行四边形,则CD=OB=4,
即|![]() a﹣4|=4,
a﹣4|=4,
解得:a=6或a=0(舍去),
故a的值为6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于F,∠CFE=∠AEB.
(1)若∠B=86°,求∠DCG的度数;
(2)AD与BC是什么位置关系?并说明理由;
(3)若∠DAB=
 ∠DGC=
∠DGC= 直接写出当
直接写出当 满足什么数量关系时,AE∥DG?
满足什么数量关系时,AE∥DG?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,对角线AC、BD交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°.
(1)求证:△AOB是等边三角形;
(2)求∠BOE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙
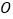 是
是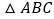 的外接圆,半径为
的外接圆,半径为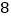 ,直线
,直线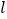 与⊙
与⊙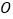 相切,切点为
相切,切点为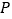 ,
,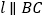 ,
,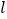 与
与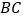 间的距离为
间的距离为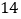 .
.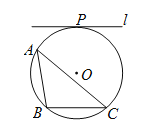
(
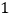 )仅用无刻度的直尺,画出一条弦,使这条弦将
)仅用无刻度的直尺,画出一条弦,使这条弦将 分成面积相等的两部分(保留作图痕迹,不写画法).
分成面积相等的两部分(保留作图痕迹,不写画法).(
 )求弦
)求弦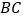 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1,可以得到
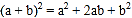 这个等式,请解答下列问题:
这个等式,请解答下列问题:
(1)写出图2中所表示的数学等式______________;(最后结果)
(2)根据整式乘法的运算法则,通过计算验证上述等式;
(3)利用(1)中得到的结论,解决问题:若a+b+c=10,ab+ac+bc=35,求a2+b2+c2的值;
(4)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张边长分别为a、b的长方形纸片拼出一个面积为(5a+2b)(3a+5b)的长方形,求x+y+z的值.
-
科目: 来源: 题型:
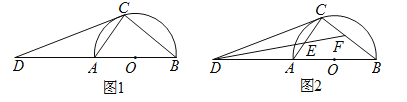
查看答案和解析>>【题目】如图
 ,
, 为半圆
为半圆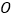 的直径,
的直径,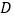 为
为 的延长线上一点,
的延长线上一点,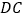 为半圆
为半圆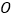 的切线,切点为
的切线,切点为 .
.
(
 )求证:
)求证: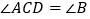 .
.(
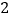 )如图
)如图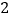 ,
,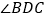 的平分线分别交
的平分线分别交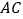 ,
,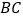 于点
于点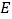 ,
,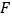 ,求
,求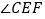 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知直线
 直线
直线 和直线
和直线 交于点C和D,在C、D之间有一点P.
交于点C和D,在C、D之间有一点P.(1)图中∠PAC、∠APB、∠PBD之间有什么关系,并说明理由;
(2)如果P点在C、D之间运动时,∠PAC、∠APB、∠PBD之间的关系是否发生变化?
(3)若点P在直线
 上C、D两点的外侧运动时(点P与点C、D不重合),试探究∠PAC、∠APB、∠PBD之间的关系又是如何?分别画出图形并说明理由。
上C、D两点的外侧运动时(点P与点C、D不重合),试探究∠PAC、∠APB、∠PBD之间的关系又是如何?分别画出图形并说明理由。
相关试题

