【题目】如图,![]() 是等腰直角三角形
是等腰直角三角形![]() 底边
底边![]() 上的高,点
上的高,点![]() 是
是![]() 的中点,延长
的中点,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() .
.
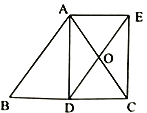
(1)求证:四边形![]() 是矩形;
是矩形;
(2)填空:
①若![]() ,
,![]() ,则四边形
,则四边形![]() 的面积=_____:
的面积=_____:
②若![]() ,则
,则![]() ____时,四边形
____时,四边形![]() 是正方形.
是正方形.
参考答案:
【答案】(1)证明见解析;(2)①120;②![]() .
.
【解析】
(1)先证明![]() ,可得OE=OD,根据平行四边形的判定得出四边形ADCE是平行四边形,根据垂直推出∠ADC=90°,可证四边形
,可得OE=OD,根据平行四边形的判定得出四边形ADCE是平行四边形,根据垂直推出∠ADC=90°,可证四边形![]() 是矩形;
是矩形;
(2)①求出DC,根据勾股定理求出AD,根据矩形的面积公式求出即可;②由正方形的判定方法可知,当CD=AD时,四边形![]() 是正方形,然后根据勾股定理列式求解即可.
是正方形,然后根据勾股定理列式求解即可.
(1)证明:∵![]() ,
,
∴![]() ,
,![]() .
.
∵点![]() 是
是![]() 的中点,
的中点,
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形.
是平行四边形.
∵![]() 是等腰三角形
是等腰三角形![]() 底边
底边![]() 上的高,∴
上的高,∴![]() ,
,
∴四边形![]() 是矩形.
是矩形.
(2) ①解:∵AD是等腰△ABC底边BC上的高,BC=16,AB=17,
∴BD=CD=8,AB=AC=17,∠ADC=90°,
由勾股定理得:AD=![]() =
=![]() =15,
=15,
∴四边形ADCE的面积是AD×DC=15×8=120;
②∵四边形![]() 是矩形,
是矩形,
∴当CD=AD时,四边形![]() 是正方形,
是正方形,
∵![]() 是等腰三角形
是等腰三角形![]() 底边
底边![]() 上的高,
上的高,
∴BD=CD,
∵BD2+AD2=AB2,
∴2BD2=100,
∴BD=5![]() ,
,
∴BC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上分别表示有理数a、b, A、B两点之间的距离表示为|AB|,利用数形结合思想回答下列问题:

(1)数轴上表示﹣3和1两点之间的距离是 ;
(2)数轴上表示x和﹣2的两点之间的距离表示为 ;
(3)若x表示一个有理数,且-3<x<1,则|x﹣1|+|x+3|的最小值是 ;
(4)若x表示一个有理数,且|x﹣1|+|x+3|>4,则有理数x的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)利用求根公式计算,结合①②③你能得出什么猜想?
①方程x2+2x+1=0的根为x1=________,x2=________,x1+x2=________,x1·x2=________.
②方程x2-3x-1=0的根为x1=________,x2=________,x1+x2=________,x1·x2=________.
③方程3x2+4x-7=0的根为x1=_______,x2=________,x1+x2=________,x1·x2=________.
(2)利用求根公式计算:一元二次方程ax2+bx+c=0(a≠0,且b2-4ac≥0)的两根为x1=________,x2=________,x1+x2=________,x1·x2=________.
(3)利用上面的结论解决下面的问题:
设x1、x2是方程2x2+3x-1=0的两个根,根据上面的结论,求下列各式的值:
①
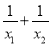 ; ②
; ②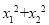 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+2分别交x,y轴于点A、C,点P是该直线与反比例函数y=
x+2分别交x,y轴于点A、C,点P是该直线与反比例函数y=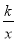 的图象,在第一象限内的交点,PB丄x轴,B为垂足,S△ABP=9.
的图象,在第一象限内的交点,PB丄x轴,B为垂足,S△ABP=9.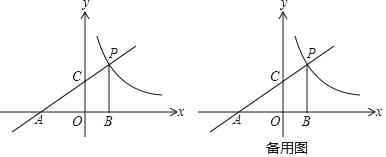
(1)直接写出点A的坐标_____;点C的坐标_____;点P的坐标_____;
(2)已知点Q在反比例函数y=
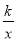 的图象上,其横坐标为6,在x轴上确定一点M,使MP+MQ最小(保留作图痕迹),并求出点M的坐标;
的图象上,其横坐标为6,在x轴上确定一点M,使MP+MQ最小(保留作图痕迹),并求出点M的坐标;(3)设点R在反比例函数y=
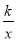 的图象上,且在直线PB的右侧,做RT⊥x轴,T为垂足,当△BRT与△AOC相似时,求点R的坐标.
的图象上,且在直线PB的右侧,做RT⊥x轴,T为垂足,当△BRT与△AOC相似时,求点R的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲加工A型零件60个所用时间和乙加工B型零件80个所用时间相同.甲、乙两人每天共加工35个零件,设甲每天加工x个A型零件.
(1)直接写出乙每天加工的零件个数;(用含x的代数式表示)
(2)求甲、乙每天各加工零件多少个?
(3)根据市场预测,加工A型零件所获得的利润为m元/件(3≤m≤5),加工B型零件所获得的利润每件比A型少1元.求甲、乙每天加工的零件所获得的总利润P(元)与m的函数关系式,并求P的最大值和最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC是ABCD的对角线,∠BAC=∠DAC.

(1)求证:AB=BC;
(2)若AB=2,AC=2
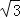 ,求ABCD的面积.
,求ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )

A. (
 ,
,  ) B. (
) B. (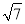 ,11) C. (2,2
,11) C. (2,2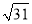 ) D. (
) D. ( ,
, 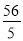 )
)
相关试题

