【题目】已知甲加工A型零件60个所用时间和乙加工B型零件80个所用时间相同.甲、乙两人每天共加工35个零件,设甲每天加工x个A型零件.
(1)直接写出乙每天加工的零件个数;(用含x的代数式表示)
(2)求甲、乙每天各加工零件多少个?
(3)根据市场预测,加工A型零件所获得的利润为m元/件(3≤m≤5),加工B型零件所获得的利润每件比A型少1元.求甲、乙每天加工的零件所获得的总利润P(元)与m的函数关系式,并求P的最大值和最小值.
参考答案:
【答案】(1)乙每天加工的零件个数为:35﹣x;(2)甲每天加工15个,乙每天加工20个;(3)P的最大值是155,最小值是85.
【解析】试题分析:
(1)由题意可得乙每天加工的零件的个数为35﹣x;
(2)根据题意可列出方程![]() ,解方程并检验即可求得所求答案了;
,解方程并检验即可求得所求答案了;
(3)由题意易得:P=15m+20(m-1)=35m-20,结合一次函数的增减性和m的取值范围即可求得P的最大值和最小值.
试题解析:
(1)∵甲、乙两人每天共加工35个零件,
∴乙每天加工的零件个数为:35﹣x;
(2)设甲每天加工x个,则乙每天加工(35﹣x)个,根据题意,得:
![]() ,解得x=15,
,解得x=15,
经检验,x=15是所列方程的解,且符合题意.
这时35﹣x=35﹣15=20,
答:甲每天加工15个,乙每天加工20个;
(3)P=15m+20(m﹣1),
即P=35m﹣20,
∵在P=35m﹣20中,P是m的一次函数,m的系数k=35>0,P随m的增大而增大,
又∵已知:3≤m≤5,
∴当m=5时,P取得最大值,P的最大值是155,
当m=3时,P取得最小值,P的最小值是85.
即P的最大值是155,最小值是85.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要测量河宽,可在两岸找到相对的两点A、B,先从B出发与AB成90°方向向前走50米,到C处立一标杆,然后方向不变继续朝前走10米到D处,在D处转90°,沿DE方向走到E处,若A、C、E三点恰好在同一直线上,且DE=17米,你能根据题目提供的数据和图形求出河宽吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度)

①请画出△A1B1C1 , 使△A1B1C1与△ABC关于原点对称;
②将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2 , 并直接写出线段OB旋转到OB2扫过图形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.
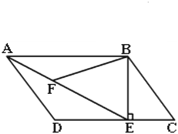
(1)ΔABF与ΔADE相似吗?说说你的理由.
(2)若AB=4,∠BAE=30°,求AE的长.
(3)在(1)、(2)的条件下,若AD=3,求BF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:

(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】雅安地震发生后,全国人民抗震救灾,众志成城,值地震发生一周年之际,某地政府又筹集了重建家园的必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型
甲
乙
丙
汽车运载量(吨/辆)
5
8
10
汽车运费(元/辆)
400
500
600
(1)全部物资可用甲型车8辆,乙型车5辆,丙型车 辆来运送.
(2)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(3)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=kx+b(k≠0)过点(1,2)
(1)填空:b= (用含k代数式表示);
(2)将此直线向下平移2个单位,设平移后的直线交x于点A,交y于点B,x轴上另有点C(1+k,0),使得△ABC的面积为2,求k值;
(3)当1≤x≤3,函数值y总大于零,求k取值范围.
相关试题

