【题目】如图,AC是ABCD的对角线,∠BAC=∠DAC.

(1)求证:AB=BC;
(2)若AB=2,AC=2![]() ,求ABCD的面积.
,求ABCD的面积.
参考答案:
【答案】(1)详见解析;(2)2![]() .
.
【解析】
试题分析:(1)根据已知条件易证∠BAC=∠BCA,即可得出AB=BC;(2)连接BD交AC于O,易证四边形ABCD是菱形,根据菱形的性质可得AC⊥BD,OA=OC=![]() AC=
AC=![]() ,OB=OD=
,OB=OD=![]() BD,根据勾股定理求出OB的长,即可得BD的长,利用ABCD的面积=
BD,根据勾股定理求出OB的长,即可得BD的长,利用ABCD的面积=![]() ACBD,即可求得答案.
ACBD,即可求得答案.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠BCA,
∵∠BAC=∠DAC,
∴∠BAC=∠BCA,
∴AB=BC;
(2)解:连接BD交AC于O,如图所示:
∵四边形ABCD是平行四边形,AB=BC,
∴四边形ABCD是菱形,
∴AC⊥BD,OA=OC=![]() AC=
AC=![]() ,OB=OD=
,OB=OD=![]() BD,
BD,
∴OB=![]() =
=![]() =1,
=1,
∴BD=2OB=2,
∴ABCD的面积=![]() ACBD=
ACBD=![]() ×2
×2![]() ×2=2
×2=2![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
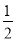 x+2分别交x,y轴于点A、C,点P是该直线与反比例函数y=
x+2分别交x,y轴于点A、C,点P是该直线与反比例函数y=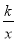 的图象,在第一象限内的交点,PB丄x轴,B为垂足,S△ABP=9.
的图象,在第一象限内的交点,PB丄x轴,B为垂足,S△ABP=9.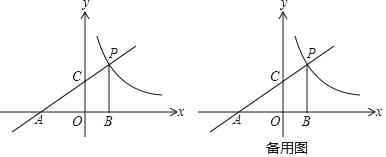
(1)直接写出点A的坐标_____;点C的坐标_____;点P的坐标_____;
(2)已知点Q在反比例函数y=
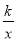 的图象上,其横坐标为6,在x轴上确定一点M,使MP+MQ最小(保留作图痕迹),并求出点M的坐标;
的图象上,其横坐标为6,在x轴上确定一点M,使MP+MQ最小(保留作图痕迹),并求出点M的坐标;(3)设点R在反比例函数y=
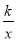 的图象上,且在直线PB的右侧,做RT⊥x轴,T为垂足,当△BRT与△AOC相似时,求点R的坐标.
的图象上,且在直线PB的右侧,做RT⊥x轴,T为垂足,当△BRT与△AOC相似时,求点R的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是等腰直角三角形
是等腰直角三角形 底边
底边 上的高,点
上的高,点 是
是 的中点,延长
的中点,延长 到
到 ,使
,使 ,连接
,连接 .
.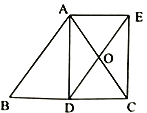
(1)求证:四边形
 是矩形;
是矩形;(2)填空:
①若
 ,
,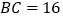 ,则四边形
,则四边形 的面积=_____:
的面积=_____:②若
 ,则
,则 ____时,四边形
____时,四边形 是正方形.
是正方形. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲加工A型零件60个所用时间和乙加工B型零件80个所用时间相同.甲、乙两人每天共加工35个零件,设甲每天加工x个A型零件.
(1)直接写出乙每天加工的零件个数;(用含x的代数式表示)
(2)求甲、乙每天各加工零件多少个?
(3)根据市场预测,加工A型零件所获得的利润为m元/件(3≤m≤5),加工B型零件所获得的利润每件比A型少1元.求甲、乙每天加工的零件所获得的总利润P(元)与m的函数关系式,并求P的最大值和最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )

A. (
 ,
,  ) B. (
) B. (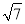 ,11) C. (2,2
,11) C. (2,2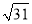 ) D. (
) D. ( ,
, 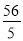 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)与x轴交于点(x1,0)与(x2,0),其中x1<x2,方程ax2+bx+c-a=0的两根为m,n(m<n),则下列判断正确的是( )
A. m<n<x1<x2 B. m<x1<x2<n C. x1+x2>m+n D. b2-4ac≥0
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲.乙两人进行跑步训练,他们所跑的路程y(米)与时间x(秒)之间的关系如图所示,则下列说法错误的是( )

A. 离终点40米处,乙追上甲B. 甲比乙迟3秒到终点
C. 甲跑步的速度是5米/秒D. 乙跑步的速度是
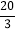 米/秒
米/秒
相关试题

