【题目】如图,点A的坐标为(8,0),点B的坐标为(6,4),点C的坐标为(0,4),点P从原点O出发,以每秒3的单位长度的速度沿x轴向右运动,点Q从点B出发,以每秒1的单位长度的速度沿线段BC向左运动,P,Q两点同时出发,当点Q运动到点C时,P,Q两点停止运动,设运动时间为t(秒).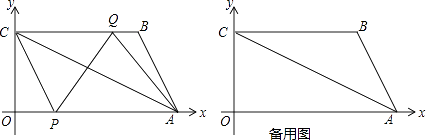
(1)当t=时,四边形OPQC为矩形;
(2)当t=时,线段PQ平分四边形OABC的面积;
(3)在整个运动过程中,当以ACPQ为顶点的四边形为平行四边形时,求该平行四边形的面积.
参考答案:
【答案】
(1)![]()
s
(2)![]()
s
(3)
解:①如图3,
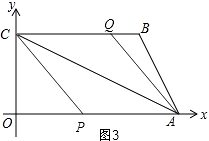
∵CQ∥AP,
∴当CQ=AP时,四边形CPAQ为平行四边形,
即:6﹣t=8﹣3t,
t=1,
∴SCPAQ=APOC=(8﹣3t)×4=(8﹣3)×4=20;
②如图4,
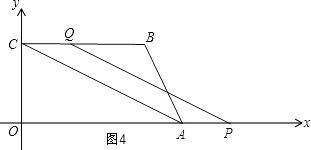
当CQ=AP时,四边形CPAQ为平行四边形,
6﹣t=3t﹣8,
t= ![]() ,
,
∴SCAPQ=APOC=(3t﹣8)×4=(3× ![]() ﹣8)×4=10;
﹣8)×4=10;
综上所述:①当t=1s时,SCPAQ=20;
②当t= ![]() s时,SCAPQ=10.
s时,SCAPQ=10.
【解析】解:(1)如图1,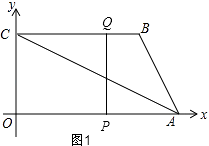
由题意得:OP=3t,BQ=t,CQ=6﹣t,
∵B(6,4),C(0,4),
∴BC∥x轴,即BC∥OP,
∵∠COP=90°,
∴当CQ=OP时,四边形OPQC为矩形,
则6﹣t=3t,
t= ![]() ,
,
所以答案是: ![]() s;
s;
·(2)如图2,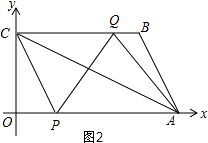
∵BC∥OA,且AB与OC不平行,
∴四边形OABC为梯形,
若线段PQ平分四边形OABC的面积,
则有:OP+CQ=BQ+AP,
3t+6﹣t=t+8﹣3t,
t= ![]() ,
,
所以答案是: ![]() s.
s.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2a-1的算术平方根是3,3a+b+4的立方根是2,求a-b的平方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示.
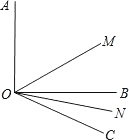
(1)已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(2)∠AOB=α,∠BOC=β,OM平分∠AOC,ON平分∠BOC,求∠MON的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线AB与反比例函数
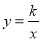 的图像相交于A,B两点,已知A(1,4).
的图像相交于A,B两点,已知A(1,4).(1)求反比例函数的解析式;
(2)直线AB交
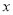 轴于点C,连结OA,当△AOC的面积为6时,求直线AB的解析式.
轴于点C,连结OA,当△AOC的面积为6时,求直线AB的解析式.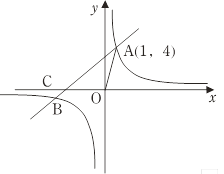
-
科目: 来源: 题型:
查看答案和解析>>【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克
0.5
1
1.5
2
2.5
3
3.5
4
烤制时间/分
40
60
80
100
120
140
160
180
设鸭的质量为x千克,烤制时间为t , 估计当x=3.2千克时,t的值为( )
A.140
B.138
C.148
D.160 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,直线AB与x轴y轴分别交于A,B两点,与双曲线y=
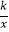 在第一象限内交于点C,BO=2AO=4,△AOC的面积为2
在第一象限内交于点C,BO=2AO=4,△AOC的面积为2 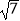 +2.
+2. 
(1)求点C的坐标和k的值;
(2)若点P在双曲线y=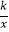 上,点Q在y轴上,且以A,B,P,Q为顶点的四边形为平行四边形,求所有符合题意的点Q的坐标.
上,点Q在y轴上,且以A,B,P,Q为顶点的四边形为平行四边形,求所有符合题意的点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式:①a0=1;②a2a3=a5;③2﹣2=﹣
 ;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0;⑤x2+x2=2x2 , 其中正确的是( )
;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0;⑤x2+x2=2x2 , 其中正确的是( )
A.①②③
B.①③⑤
C.②③④
D.②④⑤
相关试题

