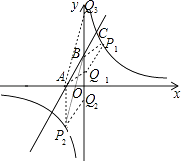
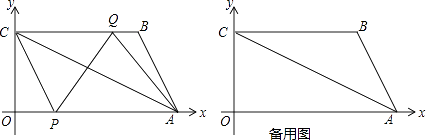
【题目】已知:如图,直线AB与x轴y轴分别交于A,B两点,与双曲线y= ![]() 在第一象限内交于点C,BO=2AO=4,△AOC的面积为2
在第一象限内交于点C,BO=2AO=4,△AOC的面积为2 ![]() +2.
+2. 
(1)求点C的坐标和k的值;
(2)若点P在双曲线y= ![]() 上,点Q在y轴上,且以A,B,P,Q为顶点的四边形为平行四边形,求所有符合题意的点Q的坐标.
上,点Q在y轴上,且以A,B,P,Q为顶点的四边形为平行四边形,求所有符合题意的点Q的坐标.
参考答案:
【答案】
(1)解:∵BO=2AO=4,
∴A(﹣2,0),B(0,4),
设直线AB的解析式为y=mx+n,
把A(﹣2,0),B(0,4)分别代入得 ![]() ,解得
,解得 ![]() ,
,
∴直线AB的解析式为y=2x+4,
设C(t,2t+4)
∵△AOC的面积为2 ![]() +2.
+2.
∴ ![]() 2(2t+4)=2
2(2t+4)=2 ![]() +2,解得t=
+2,解得t= ![]() ﹣1,
﹣1,
∴C( ![]() ﹣1,2
﹣1,2 ![]() +2),
+2),
把C( ![]() ﹣1,2
﹣1,2 ![]() +2)代入y=
+2)代入y= ![]() 得k=(
得k=( ![]() ﹣1)(2
﹣1)(2 ![]() +2)=12
+2)=12
(2)解:当平行四边形为AQPB时,把A点向右平移2个单位得到Q1点,则B点向右平移2个单位得到P1点,所以P1(2,6),即B点向右平移2个单位,再向上平移2个单位得到P1点,所以A点向右平移2个单位,再向上平移2个单位得到点Q1(0,2);
当平行四边形为APQB时,则P2(﹣2,﹣6),即点A向下平移6个单位得到点P2,则B点向下平移6个单位得到点Q2(0,﹣2);
当平行四边形为APBQ时,则P2(﹣2,﹣6),即点A向下平移6个单位得到点P2,则B点向上平移6个单位得到点Q3(0,10);
综上所述,满足条件的Q点坐标为(0,2)、(0,﹣2)、(0,10).
【解析】(1)先由BO=2AO=4得到A(﹣2,0),B(0,4),再利用待定系数法求出直线AB的解析式为y=2x+4,设C(t,2t+4),利用三角形面积公式得到 ![]() 2(2t+4)=2
2(2t+4)=2 ![]() +2,然后解方程求出t即可得到C点坐标,再利用反比例函数图像上点的坐标特征求k的值;(2)分类讨论:分AB为平行四边形的边和对角线讨论,根据平行四边形的性质,利用点平移的坐标规律求出对应的P点和Q点坐标.
+2,然后解方程求出t即可得到C点坐标,再利用反比例函数图像上点的坐标特征求k的值;(2)分类讨论:分AB为平行四边形的边和对角线讨论,根据平行四边形的性质,利用点平移的坐标规律求出对应的P点和Q点坐标.
【考点精析】掌握平行四边形的性质是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线AB与反比例函数
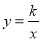 的图像相交于A,B两点,已知A(1,4).
的图像相交于A,B两点,已知A(1,4).(1)求反比例函数的解析式;
(2)直线AB交
 轴于点C,连结OA,当△AOC的面积为6时,求直线AB的解析式.
轴于点C,连结OA,当△AOC的面积为6时,求直线AB的解析式.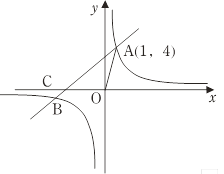
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(8,0),点B的坐标为(6,4),点C的坐标为(0,4),点P从原点O出发,以每秒3的单位长度的速度沿x轴向右运动,点Q从点B出发,以每秒1的单位长度的速度沿线段BC向左运动,P,Q两点同时出发,当点Q运动到点C时,P,Q两点停止运动,设运动时间为t(秒).
(1)当t=时,四边形OPQC为矩形;
(2)当t=时,线段PQ平分四边形OABC的面积;
(3)在整个运动过程中,当以ACPQ为顶点的四边形为平行四边形时,求该平行四边形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克
0.5
1
1.5
2
2.5
3
3.5
4
烤制时间/分
40
60
80
100
120
140
160
180
设鸭的质量为x千克,烤制时间为t , 估计当x=3.2千克时,t的值为( )
A.140
B.138
C.148
D.160 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式:①a0=1;②a2a3=a5;③2﹣2=﹣
 ;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0;⑤x2+x2=2x2 , 其中正确的是( )
;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0;⑤x2+x2=2x2 , 其中正确的是( )
A.①②③
B.①③⑤
C.②③④
D.②④⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:3x2y﹣2x3﹣2(x2y﹣x3),其中x=﹣3,y=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把直线y=﹣2x+1沿y轴向上平移2个单位,所得直线的函数关系式为_________
相关试题

