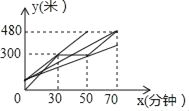
【题目】“五一”期间,小红到某景区登山游玩,小红上山时间x(分钟)与走过的路程y(米)之间的函数关系如图所示,在小红出发的同时另一名游客小卉正在距离山底60米处沿相同线路上山,若小红上山过程中与小卉恰好有两次相遇,则小卉上山平均速度v(米/分钟)的取值范围是_____.

参考答案:
【答案】6<v<8或v=4.8
【解析】
利用极限值法找出小卉走过的路程y与小红上山时间x之间的函数图象经过的点的坐标,由点的坐标利用待定系数法可求出y与x之间的函数关系式,再结合函数图象,即可找出小卉上山平均速度v(米/分钟)的取值范围.
解:设小卉走过的路程y与小红上山时间x之间的函数关系式为y=kx+b(k≠0).
将(0,60)、(30,300)代入y=kx+b,得:
![]() ,解得:
,解得:![]() ,
,
∴此种情况下,y关于x的函数关系式为y=8x+60;
将(0,60)、(70,480)代入y=kx+b,得:
![]() ,解得:
,解得:![]() ,
,
∴此种情况下,y关于x的函数关系式为y=6x+60;
将(0,60)、(50,300)代入y=kx+b,得:
![]() ,解得:
,解得:![]() ,
,
∴此种情况下,y关于x的函数关系式为y=4.8x+60.
观察图形,可知:小卉上山平均速度v(米/分钟)的取值范围是6<v<8或v=4.8.
故答案为:6<v<8或v=4.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解学生“自主学习、合作交流” 的情况,对某班部分同学进行了一段时间的跟踪调查,将调查结果(A:特别好;B:好;C:一般;D:较差)绘制成以下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:

(1)补全条形统计图;
(2)扇形统计图中,求 类所占圆心角的度数;
类所占圆心角的度数;
(3)学校想从被调查的 类(1名男生2名女生)和D类(男女生各占一半)中分别选取一位同学进行“一帮一”互助学习,请用画树形图或列表的方法求所选的两位同学恰好是一男一女的概率.
类(1名男生2名女生)和D类(男女生各占一半)中分别选取一位同学进行“一帮一”互助学习,请用画树形图或列表的方法求所选的两位同学恰好是一男一女的概率. -
科目: 来源: 题型:
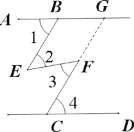
查看答案和解析>>【题目】阅读下列文字,并完成证明;
已知:如图,∠1=∠4,∠2=∠3,求证:AB∥CD;
证明:如图,延长CF交AB于点G
∵∠2=∠3
∴BE∥CF( )
∴∠1= ( )
又∠1=∠4
∴∠4= ( )
∴AB∥CD( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是⊙
是⊙  的直径,
的直径,  是⊙
是⊙  的弦,过点
的弦,过点  的切线交
的切线交  的延长线于点
的延长线于点  ,且
,且  .
.
(1)求 的度数;
的度数;
(2)若 =3,求图中阴影部分的面积.
=3,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )

A.abc<0
B.﹣3a+c<0
C.b2﹣4ac≥0
D.将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=5,AD=9,点P为AD边上点,沿BP折叠△ABP,点A的对应点为E,若点E到矩形两条较长边的距离之比为1:4,则AP的长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是
 的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )
的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )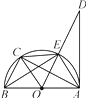
A.1个
B.2个
C.3个
D.4个
相关试题

