【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是 ![]() 的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )
的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )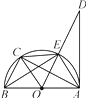
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】D
【解析】由C为 ![]() 的中点,利用垂径定理的逆定理得出OC⊥BE,由AB为圆的直径,利用直径所对的圆周角为直角得到AE⊥BE,即可确定出OC∥AE,故A正确;
的中点,利用垂径定理的逆定理得出OC⊥BE,由AB为圆的直径,利用直径所对的圆周角为直角得到AE⊥BE,即可确定出OC∥AE,故A正确;
由C为 ![]() 的中点,即
的中点,即 ![]() ,利用等弧对等弦,得到BC=EC,故B正确;
,利用等弧对等弦,得到BC=EC,故B正确;
由AD为圆的切线,得到AD⊥OA,进而确定出一对角互余,再由直角三角形ABE中两锐角互余,利用同角的余角相等,得到∠DAE=∠ABE,故C正确;
AC不一定垂直于OE,故D错误.
故答案为:D
利用垂径定理的逆定理得出OC⊥BE,由AB为圆的直径,利用直径所对的圆周角为直角得到AE⊥BE,即可确定出OC∥AE;利用等弧对等弦,得到BC=EC;利用同角的余角相等,得到∠DAE=∠ABE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,小红到某景区登山游玩,小红上山时间x(分钟)与走过的路程y(米)之间的函数关系如图所示,在小红出发的同时另一名游客小卉正在距离山底60米处沿相同线路上山,若小红上山过程中与小卉恰好有两次相遇,则小卉上山平均速度v(米/分钟)的取值范围是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )

A.abc<0
B.﹣3a+c<0
C.b2﹣4ac≥0
D.将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=5,AD=9,点P为AD边上点,沿BP折叠△ABP,点A的对应点为E,若点E到矩形两条较长边的距离之比为1:4,则AP的长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,AB∥CD,E为直线CD下方一点,BF平分∠ABE.

(1)求证:∠ABE+∠C﹣∠E=180°.
(2)如图2,EG平分∠BEC,过点B作BH∥GE,求∠FBH与∠C之间的数量关系.
(3)如图3,CN平分∠ECD,若BF的反向延长线和CN的反向延长线交于点M,且∠E+∠M=130°,请直接写出∠E的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】运动服装店销售某品牌S号,M号,L号,XL号,XXL号五种不同型号服装,随机统计该品牌运动服装一周的销售情况并绘制如图所示不完整统计图.
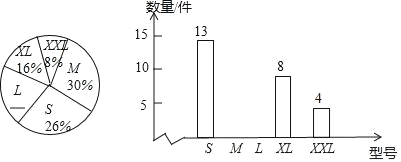
(1)L号运动服一周的销售所占百分比为 .
(2)请补全条形统计图;
(3)服装店老板打算再次购进该品牌服饰共600件,根据各种型号的销售情况,你认为购进XL号约多少件比较合适,请计算说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AF平分∠BAD交BC于E,交DC延长线于F,点G为EF的中点,连结DG.
(1)求证:BC=DF;
(2)连BD,求BD:DG的值.

相关试题

