【题目】如图, ![]() 是⊙
是⊙ ![]() 的直径,
的直径, ![]() 是⊙
是⊙ ![]() 的弦,过点
的弦,过点 ![]() 的切线交
的切线交 ![]() 的延长线于点
的延长线于点 ![]() ,且
,且 ![]() .
.
(1)求 ![]() 的度数;
的度数;
(2)若 ![]() =3,求图中阴影部分的面积.
=3,求图中阴影部分的面积.
参考答案:
【答案】
(1)解:连接OC,
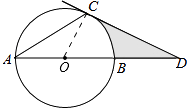
∵过点C的切线交AB的延长线于点D,
∴OC⊥CD,
∴∠OCD=90°,即∠D+∠COD=90°,
∵AO=CO,
∴∠A=∠ACO,
∴∠COD=2∠A,
∵∠A=∠D,
∴∠COD=2∠D,
∴3∠D=90°,
∴∠D=30°,
∴∠ACD=180°-∠A-∠D=180°-30°-30°=120°
(2)解:由(1)可知∠COD=60°在Rt△COD中,∵CD=3,∴OC=3× ![]() ,∴阴影部分的面积=
,∴阴影部分的面积= ![]()
【解析】(1)根据切线的性质和已知∠A=∠D,得到∠COD=2∠D,根据三角形内角和定理,求出∠ACD的度数;(2)由(1)可知∠COD=60°,求出阴影部分的面积等于三角形COD的面积-扇形COB的面积.
【考点精析】利用切线的性质定理对题目进行判断即可得到答案,需要熟知切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面
 与通道
与通道  平行),通道水平宽度
平行),通道水平宽度  为8米,
为8米,  ,通道斜面
,通道斜面  的长为6米,通道斜面
的长为6米,通道斜面  的坡度
的坡度  .
.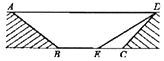
(1)求通道斜面 的长为米;
的长为米;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面 的坡度变缓,修改后的通道斜面
的坡度变缓,修改后的通道斜面  的坡角为30°,求此时
的坡角为30°,求此时  的长.(结果保留根号)
的长.(结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解学生“自主学习、合作交流” 的情况,对某班部分同学进行了一段时间的跟踪调查,将调查结果(A:特别好;B:好;C:一般;D:较差)绘制成以下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:

(1)补全条形统计图;
(2)扇形统计图中,求 类所占圆心角的度数;
类所占圆心角的度数;
(3)学校想从被调查的 类(1名男生2名女生)和D类(男女生各占一半)中分别选取一位同学进行“一帮一”互助学习,请用画树形图或列表的方法求所选的两位同学恰好是一男一女的概率.
类(1名男生2名女生)和D类(男女生各占一半)中分别选取一位同学进行“一帮一”互助学习,请用画树形图或列表的方法求所选的两位同学恰好是一男一女的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列文字,并完成证明;
已知:如图,∠1=∠4,∠2=∠3,求证:AB∥CD;
证明:如图,延长CF交AB于点G
∵∠2=∠3
∴BE∥CF( )
∴∠1= ( )
又∠1=∠4
∴∠4= ( )
∴AB∥CD( )
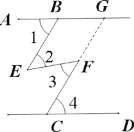
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,小红到某景区登山游玩,小红上山时间x(分钟)与走过的路程y(米)之间的函数关系如图所示,在小红出发的同时另一名游客小卉正在距离山底60米处沿相同线路上山,若小红上山过程中与小卉恰好有两次相遇,则小卉上山平均速度v(米/分钟)的取值范围是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )

A.abc<0
B.﹣3a+c<0
C.b2﹣4ac≥0
D.将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=5,AD=9,点P为AD边上点,沿BP折叠△ABP,点A的对应点为E,若点E到矩形两条较长边的距离之比为1:4,则AP的长为_____.

相关试题

