【题目】(1)(方法回顾)证明:三角形中位线定理.
已知:如图1,![]() 中,D、E分别是AB、AC的中点.
中,D、E分别是AB、AC的中点.
求证:![]() ,
,![]() .
.
证明:如图1,延长DE到点F,使得![]() ,连接CF;
,连接CF;
请继续完成证明过程;

(2)(问题解决)
如图2,在矩形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若![]() ,
,![]() ,
,![]() ,求GF的长.
,求GF的长.
(3)(思维拓展)
如图3,在梯形ABCD中,![]() ,
,![]() ,
,![]() ,E为AD的中点,G、F分别为AB、CD边上的点,若
,E为AD的中点,G、F分别为AB、CD边上的点,若![]() ,
,![]() ,
,![]() ,求GF的长.
,求GF的长.
参考答案:
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)用“倍长法”将DE延长一倍:延长DE到F,使得EF=DE,利用“边角边”证明△ADE和△CEF全等,根据全等三角形对应边相等可得AD=CF,然后判断出四边形BCFD是平行四边形,根据平行四边形的性质可得;
(2)先判断出△AEG≌△DEH(ASA),进而判断出EF垂直平分GH,即可得出结论;
(3)如图3,作辅助线构建全等三角形,先求出AG=HD=2![]() ,进而判断出△PDH为30度的直角三角形,再用勾股定理求出HF即可得出结论.
,进而判断出△PDH为30度的直角三角形,再用勾股定理求出HF即可得出结论.
(1)证明:(1)如图1,延长DE到点F,使得EF=DE,连接CF,

在△ADE和△CFE中,
 ,
,
∴△ADE≌△CFE(SAS),
∴∠A=∠ECF,AD=CF,
∴CF∥AB,
又∵AD=BD,
∴CF=BD,
∴四边形BCFD是平行四边形,
∴DE∥BC,DE=![]() BC.
BC.
(2)如图2,延长GE、FD交于点H,

∵E为AD中点,
∴EA=ED,且∠A=∠EDH=90°,
在△AEG和△DEH中,
 ,
,
∴△AEG≌△DEH(ASA),
∴AG=HD=3,EG=EH,
∵∠GEF=90°,
∴EF垂直平分GH,
∴GF=HF=DH+DF=3+7=10;
(3)解:如图3,过点D作AB的平行线交GE的延长线于点H,过H作CD的垂线,垂足为P,连接HF,

同(1)可知△AEG≌△DEH,GF=HF,
∴∠A=∠HDE=90°,AG=HD=2![]()
∵∠ADC=120°,
∴∠HDF=360°90°120°=150°,
∴∠HDP=30°,
∴PH=![]() DH=
DH=![]() ,PD=3,
,PD=3,
∴PF=PD+DF=3+4=7
在Rt△HFP中,∠HPF=90°,HP=![]() ,PF=7,
,PF=7,
∴HF=![]() =
=![]()
∴GF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有6张正面分别标有数字﹣1,0,1,2,3,4的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为a,则使得关于x的二次函数y=x2﹣2x+a﹣2与x轴有交点,且关于x的分式方程
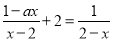 有解的概率为( )
有解的概率为( )A.
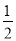 B.
B. 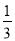 C.
C. 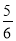 D.
D. 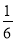
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与X轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:
①4a﹣2b+c<0;②2a﹣b<0;③a+c<1;④b2+8a>4ac,
其中正确的有( )

A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】尺规作图(不用写出作法,保留作图痕迹):
(1)在 DE 的上方,求作
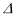 FDE,使得
FDE,使得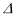 FDE≌
FDE≌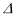 BDE;
BDE; (2)若∠B=50°,则∠ADF+∠CEF= °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个不相等的实数a,b满足a2+b2=5.
(1)若ab=2,求a+b的值;
(2)若a2﹣2a=m,b2﹣2b=m,求a+b和m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD中,点E是边AD的中点.连接BE,在BE上找一点F,连接AF,将AF绕点A顺时针旋转90°到AG,点F与点G对应.AG、BD延长线交于点H.若AB=4,当F、E、G三点共线时,求S△BFH=_____.

-
科目: 来源: 题型:
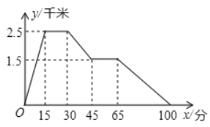
查看答案和解析>>【题目】如图反映的是小华从家里跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小华离家的距离.根据图像回答下列问题:
(1)小华在体育馆锻炼了_____分钟;
(2)体育馆离文具店______千米;
(3)小华从家跑步到体育馆,从文具店散步回家的速度分别是多少千米/分钟?
相关试题

