【题目】两个不相等的实数a,b满足a2+b2=5.
(1)若ab=2,求a+b的值;
(2)若a2﹣2a=m,b2﹣2b=m,求a+b和m的值.
参考答案:
【答案】(1)±3;(2)2,![]() .
.
【解析】
(1)先根据完全平方公式求出(a+b)2,再求出即可;
(2)两等式相加、相减,变形后求出a+b=2,再变形后代入a2+b2-2(a+b)=2m,即可求出m.
解:(1)∵a2+b2=5,ab=2,
∴(a+b)2=a2+2ab+b2=5+2×2=9,
∴a+b=±3;
(2)∵a2-2a=m,b2-2b=m,
∴a2-2a=b2-2b,a2-2a+b2-2b=2m,
∴a2-b2-2(a-b)=0,
∴(a-b)(a+b-2)=0,
∵a≠b,
∴a+b-2=0,
∴a+b=2,
∵a2-2a+b2-2b=2m,
∴a2+b2-2(a+b)=2m,
∵a2+b2=5,
∴5-2×2=2m,
解得:m=![]() ,
,
即a+b=2,m=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与X轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:
①4a﹣2b+c<0;②2a﹣b<0;③a+c<1;④b2+8a>4ac,
其中正确的有( )

A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
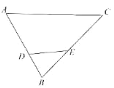
查看答案和解析>>【题目】尺规作图(不用写出作法,保留作图痕迹):
(1)在 DE 的上方,求作
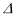 FDE,使得
FDE,使得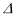 FDE≌
FDE≌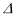 BDE;
BDE; (2)若∠B=50°,则∠ADF+∠CEF= °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)(方法回顾)证明:三角形中位线定理.
已知:如图1,
 中,D、E分别是AB、AC的中点.
中,D、E分别是AB、AC的中点.求证:
 ,
, .
.证明:如图1,延长DE到点F,使得
 ,连接CF;
,连接CF;请继续完成证明过程;

(2)(问题解决)
如图2,在矩形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若
 ,
, ,
, ,求GF的长.
,求GF的长.(3)(思维拓展)
如图3,在梯形ABCD中,
 ,
, ,
, ,E为AD的中点,G、F分别为AB、CD边上的点,若
,E为AD的中点,G、F分别为AB、CD边上的点,若 ,
, ,
, ,求GF的长.
,求GF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD中,点E是边AD的中点.连接BE,在BE上找一点F,连接AF,将AF绕点A顺时针旋转90°到AG,点F与点G对应.AG、BD延长线交于点H.若AB=4,当F、E、G三点共线时,求S△BFH=_____.

-
科目: 来源: 题型:
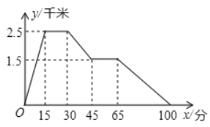
查看答案和解析>>【题目】如图反映的是小华从家里跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小华离家的距离.根据图像回答下列问题:
(1)小华在体育馆锻炼了_____分钟;
(2)体育馆离文具店______千米;
(3)小华从家跑步到体育馆,从文具店散步回家的速度分别是多少千米/分钟?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
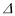 ABC 中,∠ACB=90°,AC=6cm,BC=8cm,点 P 从 A 点出发沿 A-C-B 路径向终点运动,终点为 B点;点 Q 从 B 点出发沿 B-C-A 路径向终点运动,终点为 A 点,点 P 和 Q 分别以 1cm/s 和 xcm / s 的运动速度 同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 P 和 Q 作 PE⊥ l 于 E,QF⊥ l 于 F.
ABC 中,∠ACB=90°,AC=6cm,BC=8cm,点 P 从 A 点出发沿 A-C-B 路径向终点运动,终点为 B点;点 Q 从 B 点出发沿 B-C-A 路径向终点运动,终点为 A 点,点 P 和 Q 分别以 1cm/s 和 xcm / s 的运动速度 同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 P 和 Q 作 PE⊥ l 于 E,QF⊥ l 于 F.(1)如图,当 x 2 时,设点 P 运动时间为 ts ,当点 P 在 AC 上,点 Q 在 BC 上时:
①用含 t 的式子表示 CP 和 CQ,则 CP= cm,CQ= cm;
②当 t 2 时,
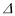 PEC 与
PEC 与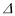 QFC 全等吗?并说明理由;
QFC 全等吗?并说明理由;(2)请问:当 x 3 时,
 PEC 与
PEC 与 QFC 有没有可能全等?若能,直接写出符合条件的 t 的值;若不能,请说明 理由。
QFC 有没有可能全等?若能,直接写出符合条件的 t 的值;若不能,请说明 理由。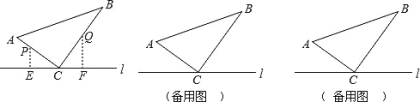
相关试题

