【题目】阅读下面材料:点A、B在数轴上分别表示有理数a、b,![]() 表示A、B两点之间的距离。当A、B两点中有一点在原点时(假设A在原点),如图①,
表示A、B两点之间的距离。当A、B两点中有一点在原点时(假设A在原点),如图①,![]() ;
;
当A、B两点都在原点右侧时,如图②,![]() ;
;
当AB两点都在原点左侧时,如图③,![]() ;
;
当AB两点在原点两侧时,如图④,![]() ;
;

请根据上述结论,回答下列问题:
(1)数轴上表示2和5的两点问距离是______,数轴上表示2和-6的两点间距高是_________,数轴上表示-1和3的两点间距离是____________.
(2)数轴上表示x和-1的两点A和B之间的距离可表示为_________,若|AB|=2,则x的值为_____________.
(3)当![]() 取最小值时,请写出所有符合条件的x的整数值_______________.
取最小值时,请写出所有符合条件的x的整数值_______________.
参考答案:
【答案】(1)3,8,4;(2)|x+1|或|x-(-1)|或|-1-x|,1或-3;(3)-2,-1,0,1
【解析】
(1)根据材料中的知识可以得到两点之间的距离就是较大的数与较小的数的差,据此即可求解;
(2)根据材料中的知识,即可直接写出结果;
(3)代数式|x-1|+|x+2|表示数轴上一点到1、-2两点的距离的和,根据两点之间线段最短,进而得出答案.
解:(1)数轴上表示2和5的两点之间的距离是:5-2=3;
数轴上表示2和-6的两点之间的距离是2-(-6)=8,
数轴上表示1和-3的两点之间的距离是1-(-3)=4;
故答案为:3;8;4;
(2)数轴上表示x和-1的两点之间的距离是|x+1|,
|AB|=2,则|x+1|=2,故x=1或-3;
故答案为:|x+1|,1或-3;
(3)若|x+1|+|x-2|取最小值,那么表示x的点M在-1和2之间的线段上,
所以x的整数值是-2,-1,0,1;
故答案为:-2,-1,0,1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据新浪网调查,在第十二届全国人大二中全会后,全国网民对政府工作报告关注度非常高,大家关注的热点话题分别有:消费、教育、环保、反腐及其它共五类,且关注五类热点问题的网民的人数所占百分比如图l所示,关注该五类热点问题网民的人数的不完整条形统计如图2,请根据图中信息解答下列问题.
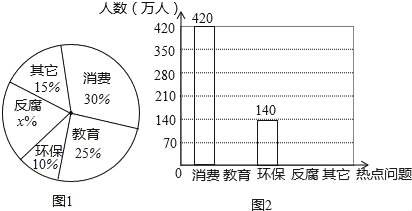
(1)求出图l中关注“反腐”类问题的网民所占百分比x的值,并将图2中的不完整的条形统计图补充完整;
(2)为了深度了解成都网民对政府工作报告的想法,新浪网邀请成都市5名网民代表甲、乙、丙、丁、戊做客新浪访谈,且一次访谈只选2名代表.请你用列表法或画树状图的方法,求出一次所选代表恰好是丙和丁的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设0!表示自然数由1到n的连乘积,并规定0!=1,Anm=
 ,nm=
,nm= (n≥0,n≥m)例如1!=1,2!=1×2=2,3!=1×2×3=6,A53=
(n≥0,n≥m)例如1!=1,2!=1×2=2,3!=1×2×3=6,A53= =60,C64=
=60,C64= =15,请回答以下问题:
=15,请回答以下问题:(1)求C32,A32;
(2)试根据C32,A32,2!的值写出C32,A32,2!满足的等量关系;试根据C43,A43,3!的值写出C43,A43,3!满足的等量关系;试根据C54,A54,4!的值写出C54,A54,4!满足的等量关系;
(3)探究Amn,Cmn与n!之间满足的等量关系(不需要证明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:O是直线AB上的一点,
 是直角,OE平分
是直角,OE平分 .
.(1)如图1.若
 .求
.求 的度数;
的度数;(2)在图1中,
 ,直接写出
,直接写出 的度数(用含a的代数式表示);
的度数(用含a的代数式表示);(3)将图1中的
 绕顶点O顺时针旋转至图2的位置,探究
绕顶点O顺时针旋转至图2的位置,探究 和
和 的度数之间的关系.写出你的结论,并说明理由.
的度数之间的关系.写出你的结论,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明到青城山游玩,乘坐缆车,当登山缆车的吊箱经过点A到达点B时,它经过了200 m,缆车行驶的路线与水平夹角∠α=16°,当缆车继续由点B到达点D时,它又走过了200 m,缆车由点B到点D的行驶路线与水平夹角∠β=42°,求缆车从点A到点D垂直上升的距离.(结果保留整数)(参考数据:sin16°≈0.27,cos16°≈0.77,sin42°≈0.66,cos42°≈0.74)

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)36+(-25)+12+(-15);
(2) 9+(-2.5)+(+6)+(-3.5);
(3)3.7+(-9.1)+6.3+(-0.9) ;
(4)10-(-5)-(-6)-(+18)
(5)(-12)-6-(-8)-(-12);
(6)5-(-5)+(-10)+0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,4),点A为MN的中点,反比例函数y=
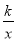 (x>0)的图象过点A.
(x>0)的图象过点A.(1)求直线l和反比例函数的解析式;
(2)在函数y=
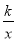 (k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.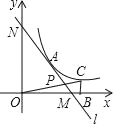
相关试题

