【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点M(﹣2, ![]() ),顶点坐标为N(﹣1,
),顶点坐标为N(﹣1, ![]() ),且与x轴交于A、B两点,与y轴交于C点.
),且与x轴交于A、B两点,与y轴交于C点.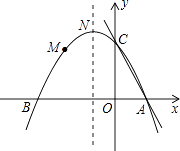
(1)求抛物线的解析式;
(2)点P为抛物线对称轴上的动点,当△PBC为等腰三角形时,求点P的坐标;
(3)在直线AC上是否存在一点Q,使△QBM的周长最小?若存在,求出Q点坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:由抛物线顶点坐标为N(﹣1, ![]() ),可设其解析式为y=a(x+1)2+
),可设其解析式为y=a(x+1)2+ ![]() ,
,
将M(﹣2, ![]() )代入,得
)代入,得 ![]() =a(﹣2+1)2+
=a(﹣2+1)2+ ![]() ,
,
解得a=﹣ ![]() ,
,
故所求抛物线的解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]()
(2)
解:∵y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() ,
,
∴x=0时,y= ![]() ,
,
∴C(0, ![]() ).
).
y=0时,﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() =0,
=0,
解得x=1或x=﹣3,
∴A(1,0),B(﹣3,0),
∴BC= ![]() =2
=2 ![]() .
.
设P(﹣1,m),
当CP=CB时,有CP= ![]() =2
=2 ![]() ,解得m=
,解得m= ![]() ±
± ![]() ;
;
当BP=BC时,有BP= ![]() =2
=2 ![]() ,解得m=±2
,解得m=±2 ![]() ;
;
当PB=PC时, ![]() =
= ![]() ,解得m=0,
,解得m=0,
综上,当△PBC为等腰三角形时,点P的坐标为(﹣1, ![]() +
+ ![]() ),(﹣1,
),(﹣1, ![]() ﹣
﹣ ![]() ),(﹣1,2
),(﹣1,2 ![]() ),(﹣1,﹣2
),(﹣1,﹣2 ![]() ),(﹣1,0)
),(﹣1,0)
(3)
解:由(2)知BC=2 ![]() ,AC=2,AB=4,
,AC=2,AB=4,
所以BC2+AC2=AB2,即BC⊥AC.
连结BC并延长至B′,使B′C=BC,连结B′M,交直线AC于点Q,
∵B、B′关于直线AC对称,
∴QB=QB′,
∴QB+QM=QB′+QM=MB′,
所以此时△QBM的周长最小.
由B(﹣3,0),C(0, ![]() ),易得B′(3,2
),易得B′(3,2 ![]() ).
).
设直线MB′的解析式为y=kx+n,
将M(﹣2, ![]() ),B′(3,2
),B′(3,2 ![]() )代入,
)代入,
得 ![]() ,解得
,解得 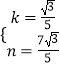 ,
,
即直线MB′的解析式为y= ![]() x+
x+ ![]() .
.
同理可求得直线AC的解析式为y=﹣ ![]() x+
x+ ![]() .
.
由 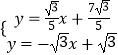 ,解得
,解得 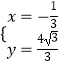 ,即Q(﹣
,即Q(﹣ ![]() ,
, ![]() ).
).
所以在直线AC上存在一点Q(﹣ ![]() ,
, ![]() ),使△QBM的周长最小.
),使△QBM的周长最小.
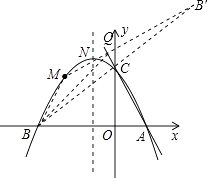
【解析】(1)先由抛物线的顶点坐标为N(﹣1, ![]() ),可设其解析式为y=a(x+1)2+
),可设其解析式为y=a(x+1)2+ ![]() ,再将M(﹣2,
,再将M(﹣2, ![]() )代入,得
)代入,得 ![]() =a(﹣2+1)2+
=a(﹣2+1)2+ ![]() ,解方程求出a的值即可得到抛物线的解析式;(2)先求出抛物线y=﹣
,解方程求出a的值即可得到抛物线的解析式;(2)先求出抛物线y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() 与x轴交点A、B,与y轴交点C的坐标,再根据勾股定理得到BC=
与x轴交点A、B,与y轴交点C的坐标,再根据勾股定理得到BC= ![]() =2
=2 ![]() .设P(﹣1,m),当△PBC为等腰三角形时分三种情况进行讨论:①CP=CB;②BP=BC;③PB=PC;(3)先由勾股定理的逆定理得出BC⊥AC,连结BC并延长至B′,使B′C=BC,连结B′M,交直线AC于点Q,由轴对称的性质可知此时△QBM的周长最小,由B(﹣3,0),C(0,
.设P(﹣1,m),当△PBC为等腰三角形时分三种情况进行讨论:①CP=CB;②BP=BC;③PB=PC;(3)先由勾股定理的逆定理得出BC⊥AC,连结BC并延长至B′,使B′C=BC,连结B′M,交直线AC于点Q,由轴对称的性质可知此时△QBM的周长最小,由B(﹣3,0),C(0, ![]() ),根据中点坐标公式求出B′(3,2
),根据中点坐标公式求出B′(3,2 ![]() ),再运用待定系数法求出直线MB′的解析式为y=
),再运用待定系数法求出直线MB′的解析式为y= ![]() x+
x+ ![]() ,直线AC的解析式为y=﹣
,直线AC的解析式为y=﹣ ![]() x+
x+ ![]() ,然后解方程组
,然后解方程组 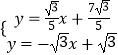 ,即可求出Q点的坐标.
,即可求出Q点的坐标.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足
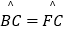 ,过点C作⊙O的切线交AB的延长线于D点,交AF的延长线于E点.
,过点C作⊙O的切线交AB的延长线于D点,交AF的延长线于E点. 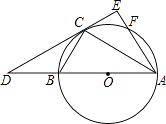
(1)求证:AE⊥DE;
(2)若tan∠CBA=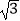 ,AE=3,求AF的长.
,AE=3,求AF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
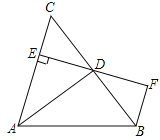
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.

(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其顶点Q落在线段AE上,定点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N。
(1)求证:MN=AM+BN;

(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC沿射线BC方向平移3cm得到△DEF.若△ABC的周长为14cm,则四边形ABFD的周长为( )

A. 14cm B. 17cm C. 20cm D. 23cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学在计算3(4+1)(42+1)时,把3写成(4﹣1)后,发现可以连续运用平方差公式计算:3(4+1)(42+1)=(4﹣1)(4+1)(42+1)=(42﹣1)(42+1)=(42)2﹣12=256﹣1=255.请借鉴该同学的方法计算(2+1)(22+1)(24+1)(28+1)…(22048+1)=______
相关试题

