【题目】小芳从家骑自行车去学校,所需时间y(min)与骑车速度x(m/min)之间的反比例函数关系如图.
(1)小芳家与学校之间的距离是多少?
(2)写出y与x的函数表达式;
(3)若小芳7点20分从家出发,预计到校时间不超过7点28分,请你用函数的性质说明小芳的骑车速度至少为多少?

参考答案:
【答案】(1)2400m;(2)y=![]() ;(3)小芳的骑车速度至少为300m/min.
;(3)小芳的骑车速度至少为300m/min.
【解析】(1)根据图象中的速度与时间即可得路程;
(2)用待定系数法即可得函数表达式;
(3)观察函数图象,根据函数的性质知在第一象限内,y随着x的增大而减小即可求得.
(1)小芳家与学校之间的距离为240×10=2400m;
(2)设y=![]() ,当x=240时,y=10,
,当x=240时,y=10,
解得k=2400,∴y=![]() ;
;
(3)当y=8时,x=300,
∵k>0,∴在第一象限内y随x的增大而减小,
∴小芳的骑车速度至少为300m/min.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)2(10﹣0.5y)=﹣(1.5y+2)
(2)
 (x﹣5)=3﹣
(x﹣5)=3﹣ (x﹣5)
(x﹣5)(3)
 ﹣1=
﹣1=
(4)x﹣
 (x﹣9)=
(x﹣9)= [x+
[x+ (x﹣9)]
(x﹣9)](5)
 -
- =0.5x+2
=0.5x+2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.
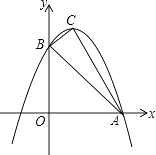
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;
(3)将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△ABC重叠部分的面积记为S,用m的代数式表示S. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市电力部门对一般照明用电实行“阶梯电价”收费,具体收费标准如下:
第一档:月用电量不超过240度的部分的电价为每度0.6元;
第二档:月用电量超过240度但不超过400度部分的电价为每度0.65元;
第三档:月用电量超过400度的部分的电价为每度0.9元.
(1)已知老王家去年5月份的用电量为380度,则老王家5月份应交电费 元;
(2)若去年6月份老王家用电的平均电价为0.70元,求老王家去年6月份的用电量;
(3)已知老王家去年7、8月份的用电量共500度(7月份的用电量少于8月份的用电量),两个月的总电价是303元,求老王家7、8月的用电量分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从一艘船的点A处观测海岸上高为41m的灯塔BC(观测点A与灯塔底部C在一个水平面上),测得灯塔顶部B的仰角为35°,则观测点A到灯塔BC的距离为 . (精确到1m)
【参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7】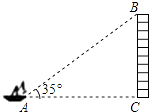
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在长方形ABCD中,AB=12cm,BC=8cm,点P从A点出发,沿A→B→C→D路线运动,到D点停止;点Q从D点出发,沿D→C→B→A运动,到A点停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,用x(秒)表示运动时间.
(1)求点P和点Q相遇时的x值.
(2)连接PQ,当PQ平分矩形ABCD的面积时,求运动时间x值.
(3)若点P、点Q运动到6秒时同时改变速度,点P的速度变为每秒3cm,点Q的速度为每秒1cm,求在整个运动过程中,点P、点Q在运动路线上相距路程为20cm时运动时间x值.
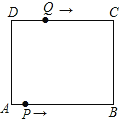


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为 .

相关试题

