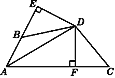
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC;
(2)猜想写出AB+AC与AE之间的数量关系并给予证明.
参考答案:
【答案】(1)证明见解析;(2)AB+AC=2AE.证明见解析.
【解析】试题分析:(1)、根据垂直得出△BDE与△CDE均为直角三角形,然后根据BD=CD,BE=CF得出三角形全等,从而得出DE=DF,根据角平分线的逆定理得出答案;(2)、根据角平分线得出∠EAD=∠CAD,结合∠E=∠AFD=90°得出∠ADE=∠ADF,从而说明△AED≌△AFD,根据全等得出AE=AF,最后根据AB+AC=AE﹣BE+AF+CF得出答案.
试题解析:(1)、∵DE⊥AB于E,DF⊥AC于F, ∴∠E=∠DFC=90°,∴△BDE与△CDE均为直角三角形,
∵![]() ,∴△BDE≌△CDF, ∴DE=DF,即AD平分∠BAC;
,∴△BDE≌△CDF, ∴DE=DF,即AD平分∠BAC;
、AB+AC=2AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程kx2-2x+1=0有实数根,则k的取值范围是( ).
A.k<1B.k≤1C.k≤1且k≠0D.k<1且k≠0
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为________厘米/秒.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知α,β是一元二次方程x2﹣5x﹣2=0的两个实数根,则α2+αβ+β2的值为( )
A.﹣1B.9C.23D.27
-
科目: 来源: 题型:
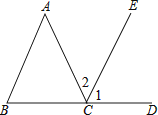
查看答案和解析>>【题目】如图,BCD是一条直线,∠1=∠B,∠2=∠A,指出∠1的同位角,∠2的内错角,并求出∠A+∠B+∠ACB的度数.
-
科目: 来源: 题型:
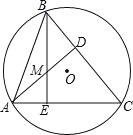
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AD⊥BC,BE⊥AC,AD,BE相交于点M,若AC=8,BM=4,则⊙O的半径等于( )
A.2
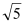 B.2
B.2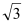 C.4
C.4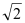 D.6
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题中,真命题有( )
①两条直线被第三条直线所截,内错角相等;
②如果∠1和∠2是对顶角,那么∠1=∠2;
③三角形的一个外角大于任何一个内角;
④若a2=b2,则a=b.
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

