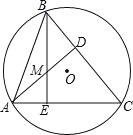
【题目】如图,△ABC内接于⊙O,AD⊥BC,BE⊥AC,AD,BE相交于点M,若AC=8,BM=4,则⊙O的半径等于( )
A.2![]() B.2
B.2![]() C.4
C.4![]() D.6
D.6
参考答案:
【答案】A
【解析】
试题分析:作直径AH,连接HB、HC,作OF⊥AC于F,连接CM,延长CM交AB于点N,则CN⊥AB,推出∠HCA=∠HBA=90°,证出四边形HBMC为平行四边形,求出HC,根据垂径定理求出AF,根据中位线得出OF,再根据勾股定理求出OA即可. 作直径AH,连接HB、HC,作OF⊥AC于F,连接CM,延长CM交AB于点N,则CN⊥AB,如图所示: ∵AH为直径, ∴∠HCA=∠HBA=90°, ∵CN⊥AB,BE⊥AC,
∴∠CNA=∠BEA=90° ∴∠HBA=∠CNA,∠HCA=∠BEA, ∴HB∥CN,HC∥BE, ∴四边形HBMC为平行四边形, ∴BM=HC=4, ∵OF⊥CC,OF过O, ∴根据垂径定理:CF=FA=![]() AC=4, ∵AO=OH, ∴OF为△ACH的中位线, ∴OF=
AC=4, ∵AO=OH, ∴OF为△ACH的中位线, ∴OF=![]() HC=2, ∴在Rt△AOF中,OA2=OF2+AF2=22+42=20, ∴AC=2
HC=2, ∴在Rt△AOF中,OA2=OF2+AF2=22+42=20, ∴AC=2![]() ;
;

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知α,β是一元二次方程x2﹣5x﹣2=0的两个实数根,则α2+αβ+β2的值为( )
A.﹣1B.9C.23D.27
-
科目: 来源: 题型:
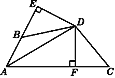
查看答案和解析>>【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC;
(2)猜想写出AB+AC与AE之间的数量关系并给予证明.
-
科目: 来源: 题型:
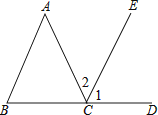
查看答案和解析>>【题目】如图,BCD是一条直线,∠1=∠B,∠2=∠A,指出∠1的同位角,∠2的内错角,并求出∠A+∠B+∠ACB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题中,真命题有( )
①两条直线被第三条直线所截,内错角相等;
②如果∠1和∠2是对顶角,那么∠1=∠2;
③三角形的一个外角大于任何一个内角;
④若a2=b2,则a=b.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,根据图形填空.
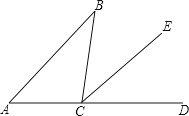
(1)∠A,是同位角;
(2)∠B和,是内错角;
(3)∠A和,__ ,是同旁内角. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
① △ABE的面积与△BCE的面积相等;② ∠AFG=∠AGF;③ ∠FAG=2∠ACF;④ BH=CH
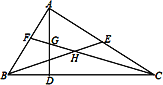
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
相关试题

