【题目】如图,边长为2的等边△ABC和边长为1的等边△A′B′C′,它们的边B′C′,BC位于同一条直线l上,开始时,点C′与B重合,△ABC固定不动,然后把△A′B′C′自左向右沿直线l平移,移出△ABC外(点B′与C重合)停止,设△A′B′C′平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )
A.
B.
C.
D.
参考答案:
【答案】B
【解析】解:如图1所示:当0<x≤1时,过点D作DE⊥BC′.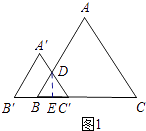
∵△ABC和△A′B′C′均为等边三角形,
∴△DBC′为等边三角形.
∴DE= ![]() BC′=
BC′= ![]() x.
x.
∴y= ![]() BC′DE=
BC′DE= ![]() x2 .
x2 .
当x=1时,y= ![]() ,且抛物线的开口向上.
,且抛物线的开口向上.
如图2所示:1<x≤2时,过点A′作A′E⊥B′C′,垂足为E.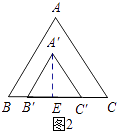
∵y= ![]() B′C′A′E=
B′C′A′E= ![]() ×1×
×1× ![]() =
= ![]() .
.
∴函数图象是一条平行与x轴的线段.
如图3所示:2<x≤3时,过点D作DE⊥B′C,垂足为E.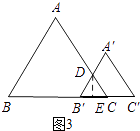
y= ![]() B′CDE=
B′CDE= ![]() (x﹣3)2 , 函数图象为抛物线的一部分,且抛物线开口向上.
(x﹣3)2 , 函数图象为抛物线的一部分,且抛物线开口向上.
故选:B.
分为0<x≤1、1<x≤2、2<x≤3三种情况画出图形,然后依据等边三角形的性质和三角形的面积公式可求得y与x的函数关系式,于是可求得问题的答案.
-
科目: 来源: 题型:
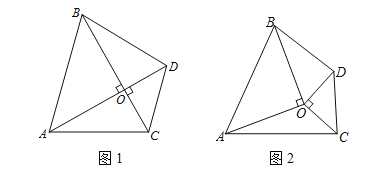
查看答案和解析>>【题目】在△OAB中,OA=OB,OA⊥OB.在△OCD中,OC=OD,OC⊥OD.
(1)如图1,若A,O,D三点在同一条直线上,求证:S△AOC=S△BOD;
(2)如图2,若A,O,D三点不在同一条直线上,△OAB和△OCD不重叠.则S△AOC=S△BOD是否仍成立?若成立,请予以证明;若不成立,也请说明理由.
(3)若A,O,D三点不在同一条直线上,△OAB和△OCD有部分重叠,经过画图猜想,请直接写出 S△AOC和S△BOD的大小关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与直线y=
 x﹣3交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
x﹣3交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.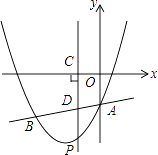
(1)求抛物线的解析式;
(2)以O,A,P,D为顶点的平行四边形是否存在?如存在,求点P的坐标;若不存在,说明理由.
(3)当点P运动到直线AB下方某一处时,过点P作PM⊥AB,垂足为M,连接PA使△PAM为等腰直角三角形,请直接写出此时点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC.
(1)请按如下步骤用直尺和圆规作图(保留作图痕迹并在图中标注字母):
①作∠ABC的平分线交AC边于点D;
②在BC的延长线上截取CE=CD;
③连接DE.
(2)求证:BD=DE.
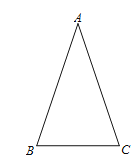
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为 .
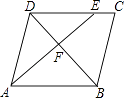
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明抛硬币的过程(每枚硬币只有正面朝上和反面朝上两种情况)见下表,阅读并回答问题:
抛掷结果
10次
50次
500次
5000次
出现正面次数
3
24
258
2498
出现正面的频率
30%
48%
51.6%
49.96%
(1)从表中可知,当抛完10次时正面出现3次,正面出现的频率为30%,那么,小明抛完10次时,得到 次反面,反面出现的频率是 ;
(2)当他抛完5000次时,反面出现的次数是 ,反面出现的频率是 ;
(3)通过上表我们可以知道,正面出现的频数和反面出现的频数之和等于
,正面出现的频率和反面出现的频率之和等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,广宇购物中心设立了一个可以自由转动的转盘,并规定:顾客购物满20元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据.
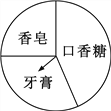
转动转盘的次数n
100
200
400
500
1000
落在“牙膏”区域的次数m
32
58
121
149
300
落在“牙膏”区域的频率
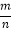
0.3025
(1)计算并完成上面的表格;
(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动该转盘一次,你获得牙膏的概率是多少?
相关试题

