【题目】在△OAB中,OA=OB,OA⊥OB.在△OCD中,OC=OD,OC⊥OD.
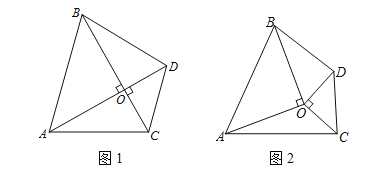
(1)如图1,若A,O,D三点在同一条直线上,求证:S△AOC=S△BOD;
(2)如图2,若A,O,D三点不在同一条直线上,△OAB和△OCD不重叠.则S△AOC=S△BOD是否仍成立?若成立,请予以证明;若不成立,也请说明理由.
(3)若A,O,D三点不在同一条直线上,△OAB和△OCD有部分重叠,经过画图猜想,请直接写出 S△AOC和S△BOD的大小关系.
参考答案:
【答案】(1)答案见解析;(2)S△AOC=S△BOD仍成立;(3)S△AOC=S△BOD.
【解析】试题分析:(1)由OA=OB,OC=OD,再结合三角形面积公式即可得到结论;
(2)作DE⊥OB于E,作CF⊥OA交AO的延长线于F.通过证明
△OED≌△OFC,得到DE=CF,再由三角形面积公式即可得到结论;
(3)类似(2)可得结论.
试题解析:解:(1)∵A,O,D三点在一条直线上,OA⊥OB,OC⊥OD,∴∠BOD=∠AOC=90°,∴S△AOC=![]() OAOC,S△BOD=
OAOC,S△BOD=![]() OBOD.
OBOD.
∵OA=OB,OC=OD,∴S△AOC=S△BOD.
(2)S△AOC=S△BOD仍成立.证明如下:
作DE⊥OB于E,作CF⊥OA交AO的延长线于F.
∵∠BOF=∠COD=90°,∴∠BOD=∠COF.
在△OED和△OFC中, 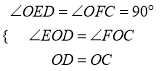 ,
,
∴△OED≌△OFC(AAS),∴DE=CF,∴S△AOC=![]() OACF,S△BOD=
OACF,S△BOD=![]() OBDE,
OBDE,
∴S△AOC=S△BOD.
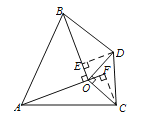
(3)S△AOC=S△BOD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小虫从某点o出发在一条直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,爬过的各段路程(单位:厘米)依次为
 ,
,




 通过计算说明小虫是否回到起点?如果小虫爬行的速度0.5厘米/秒,小虫共爬行了多少时间?
通过计算说明小虫是否回到起点?如果小虫爬行的速度0.5厘米/秒,小虫共爬行了多少时间? -
科目: 来源: 题型:
查看答案和解析>>【题目】杨梅是漳州的特色时令水果,杨梅一上市,水果店的老板用1200元购进一批杨梅,很快售完;老板又用2500元购进第二批杨梅,所购件数是第一批的2倍,但进价比第一批每件多了5元.
(1)第一批杨梅每件进价多少元?
(2)老板以每件150元的价格销售第二批杨梅,售出80%后,为了尽快售完,决定打折促销,要使第二批杨梅的销售利润不少于320元,剩余的杨梅每件售价至少打几折?(利润=售价﹣进价) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形 ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.

(1)求AO的长;
(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC= AM;
AM;
(3)连接EM,若△AEM的面积为40,请直接写出△AFM的周长.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与直线y=
 x﹣3交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
x﹣3交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.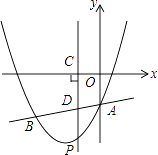
(1)求抛物线的解析式;
(2)以O,A,P,D为顶点的平行四边形是否存在?如存在,求点P的坐标;若不存在,说明理由.
(3)当点P运动到直线AB下方某一处时,过点P作PM⊥AB,垂足为M,连接PA使△PAM为等腰直角三角形,请直接写出此时点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC.
(1)请按如下步骤用直尺和圆规作图(保留作图痕迹并在图中标注字母):
①作∠ABC的平分线交AC边于点D;
②在BC的延长线上截取CE=CD;
③连接DE.
(2)求证:BD=DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2的等边△ABC和边长为1的等边△A′B′C′,它们的边B′C′,BC位于同一条直线l上,开始时,点C′与B重合,△ABC固定不动,然后把△A′B′C′自左向右沿直线l平移,移出△ABC外(点B′与C重合)停止,设△A′B′C′平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )

A.
B.
C.
D.
相关试题

