【题目】如图,在△ABC中,AB=AC.
(1)请按如下步骤用直尺和圆规作图(保留作图痕迹并在图中标注字母):
①作∠ABC的平分线交AC边于点D;
②在BC的延长线上截取CE=CD;
③连接DE.
(2)求证:BD=DE.
参考答案:
【答案】(1)答案见解析;(2)答案见解析.
【解析】试题分析:(1)根据语句作出图形即可;
(2)根据等边对等角得到∠ABC=∠ACB和∠CDE=∠CED.再由角平分线的性质得到∠ABC=2∠CBD.由三角形外角的性质得到∠ACB=∠CDE+∠CED=2∠CED,从而得到∠CBD=∠CED,再由等角对等边即可得到结论.
试题解析:解:(1)如图所示:
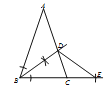
(2)∵AB=AC,∴∠ABC=∠ACB.
∵CD=CE,∴∠CDE=∠CED.
∵BD平分∠ABC,∴∠ABC=2∠CBD.
又∵∠ACB=∠CDE+∠CED=2∠CED,
∴∠CBD=∠CED,∴BD=DE.
-
科目: 来源: 题型:
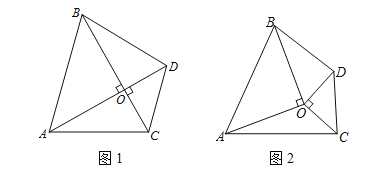
查看答案和解析>>【题目】如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形 ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.

(1)求AO的长;
(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC= AM;
AM;
(3)连接EM,若△AEM的面积为40,请直接写出△AFM的周长.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答 -
科目: 来源: 题型:
查看答案和解析>>【题目】在△OAB中,OA=OB,OA⊥OB.在△OCD中,OC=OD,OC⊥OD.
(1)如图1,若A,O,D三点在同一条直线上,求证:S△AOC=S△BOD;
(2)如图2,若A,O,D三点不在同一条直线上,△OAB和△OCD不重叠.则S△AOC=S△BOD是否仍成立?若成立,请予以证明;若不成立,也请说明理由.
(3)若A,O,D三点不在同一条直线上,△OAB和△OCD有部分重叠,经过画图猜想,请直接写出 S△AOC和S△BOD的大小关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与直线y=
 x﹣3交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
x﹣3交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.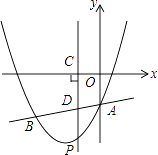
(1)求抛物线的解析式;
(2)以O,A,P,D为顶点的平行四边形是否存在?如存在,求点P的坐标;若不存在,说明理由.
(3)当点P运动到直线AB下方某一处时,过点P作PM⊥AB,垂足为M,连接PA使△PAM为等腰直角三角形,请直接写出此时点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2的等边△ABC和边长为1的等边△A′B′C′,它们的边B′C′,BC位于同一条直线l上,开始时,点C′与B重合,△ABC固定不动,然后把△A′B′C′自左向右沿直线l平移,移出△ABC外(点B′与C重合)停止,设△A′B′C′平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
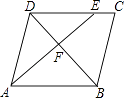
查看答案和解析>>【题目】如图所示,在ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明抛硬币的过程(每枚硬币只有正面朝上和反面朝上两种情况)见下表,阅读并回答问题:
抛掷结果
10次
50次
500次
5000次
出现正面次数
3
24
258
2498
出现正面的频率
30%
48%
51.6%
49.96%
(1)从表中可知,当抛完10次时正面出现3次,正面出现的频率为30%,那么,小明抛完10次时,得到 次反面,反面出现的频率是 ;
(2)当他抛完5000次时,反面出现的次数是 ,反面出现的频率是 ;
(3)通过上表我们可以知道,正面出现的频数和反面出现的频数之和等于
,正面出现的频率和反面出现的频率之和等于 .
相关试题

