【题目】为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下,请将有关问题补充完整.
收集数据:随机抽取甲乙两所学校的20名学生的数学成绩进行分析:
甲 | 91 | 89 | 77 | 86 | 71 | 31 | 97 | 93 | 72 | 91 |
81 | 92 | 85 | 85 | 95 | 88 | 88 | 90 | 44 | 91 | |
乙 | 84 | 93 | 66 | 69 | 76 | 87 | 77 | 82 | 85 | 88 |
90 | 88 | 67 | 88 | 91 | 96 | 68 | 97 | 59 | 88 |
整理、描述数据:按如下数据段整理、描述这两组数据
分段 学校 | 30≤x≤39 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 |
|
|
|
|
|
|
|
分析数据:两组数据的平均数、中位数、众数、方差如下表:
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 81.85 | 88 | 91 | 268.43 |
乙 | 81.95 | 86 | m | 115.25 |
经统计,表格中m的值是 .
得出结论:
a若甲学校有400名初二学生,估计这次考试成绩80分以上人数为 .
b可以推断出 学校学生的数学水平较高,理由为 .(至少从两个不同的角度说明推断的合理性)
参考答案:
【答案】见解析
【解析】分析:(1)根据收集的数据即可填写表格;
(2)根据众数的定义:一组数据中出现次数最多的数据就叫这组数据的众数,即可求出m;
(3)a:用甲学校样本中80分以上的人数除以20再乘以400即可得出答案;
b:根据情况进行讨论分析,理由合理即可.
详解:(1)整理、描述数据
分段 学校 | 30≤x≤39 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 | 0 | 0 | 1 | 4 | 2 | 8 | 5 |
(2)乙学校20名学生的数学成绩中,88出现的次数最多是这组数据的众数,
故答案为:88.
(3)a:甲学校样本中80分以上的人数有7+8=15(人),
占样本的![]() ,
,
所以若甲学校有400名初二学生,估计这次考试成绩80分以上人数为: ![]() (人),
(人),
故答案为:300;
b:答案不唯一,理由须支撑推断结论.
-
科目: 来源: 题型:
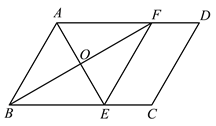
查看答案和解析>>【题目】如图,在□ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形;
(2)连接CF,若∠ABC=60°,AB= 4,AF =2DF,求CF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形纸片ABCD中,AB=6 cm,BC=8 cm,点E是BC边上一点,连接AE,并将△AEB沿AE折叠,得到△AEB′,以C,E,B′为顶点的三角形是直角三角形时,BE的长为____cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC∽正方形ODEF,它们是以原点O为位似中心的位似图形,位似比为1:
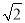 , 点A的坐标为(0,1),则点E的坐标是________或________.
, 点A的坐标为(0,1),则点E的坐标是________或________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图案是由火柴棒按某种规律搭成的第(1)个图案中有2个正方形,第(2)个图案中有5个正方形,第(3)个图案中有8个正方形,以此类推……
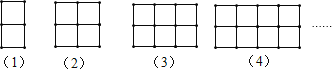
根据上面规律,
(1)第(5)个图案中有 个正方形;
(2)第n个图案中有 个正方形;
(3)小明同学说照此规律搭成的图案中,能得到2019个正方形,你认为他的结论正确吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°
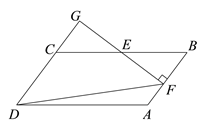
(1)求证:GD=GF.
(2)已知BC=10,
 .求 CD的长.
.求 CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC与△A′B′C′关于点P位似,且顶点都在格点上.
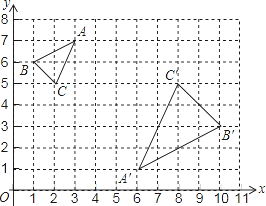
(1)在图上找出位似中心P的位置,并直接写出点P的坐标是;
(2)写出△ABC与△A′B′C′的面积比.
相关试题

