【题目】如图,长方形纸片ABCD中,AB=6 cm,BC=8 cm,点E是BC边上一点,连接AE,并将△AEB沿AE折叠,得到△AEB′,以C,E,B′为顶点的三角形是直角三角形时,BE的长为____cm.

参考答案:
【答案】3或6
【解析】试题解析:①∠B′EC=90°时,如图1,∠BEB′=90°,
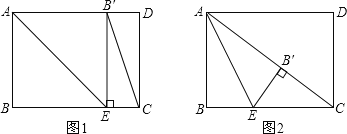
由翻折的性质得∠AEB=∠AEB′=![]() ×90°=45°,
×90°=45°,
∴△ABE是等腰直角三角形,
∴BE=AB=6cm;
②∠EB′C=90°时,如图2,
由翻折的性质∠AB′E=∠B=90°,
∴A、B′、C在同一直线上,
AB′=AB,BE=B′E,
由勾股定理得,AC=![]() =10cm,
=10cm,
∴B′C=10-6=4cm,
设BE=B′E=x,则EC=8-x,
在Rt△B′EC中,B′E2+B′C2=EC2,
即x2+42=(8-x)2,
解得x=3,
即BE=3cm,
综上所述,BE的长为3或6cm.
故答案为:3或6.
-
科目: 来源: 题型:
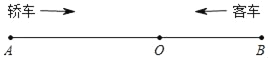
查看答案和解析>>【题目】如图,A,B两地相距450千米,两地之间有一个加油站O,且AO=270千米,一辆轿车从A地出发,以每小时90千米的速度开往B地,一辆客车从B地出发,以每小时60千米的速度开往A地,两车同时出发,设出发时间为t小时.
(1)经过几小时两车相遇?
(2)当出发2小时时,轿车和客车分别距离加油站O多远?
(3)经过几小时,两车相距50千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)计算:(π﹣3.14)0+( )﹣1+|﹣2
)﹣1+|﹣2 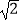 |﹣
|﹣ 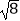 .
.
(2)先化简,再求值: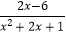 ÷(
÷( 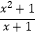 ﹣x+1),并从﹣tan60°≤x≤2cos30°取出一个合适的整数,求出式子的值.
﹣x+1),并从﹣tan60°≤x≤2cos30°取出一个合适的整数,求出式子的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b分别对应数轴上A、B两点,并且满足|a﹣2|+(3a+2b)2=0,点P为数轴上一个动点,它对应的数是x
(1)填空:a= ,b= ,AB= ;
(2)若P为线段AB上一点,并且PA=3PB,求x的值;
(3)若P点从A点出发以每秒2个单位的速度运动,那么出发几秒钟后,线段PA=4PB?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.

(1)求证:BE=CE.
(2)求∠BEC的度数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由边长为1的小正三角形组成的网格图,点O和△ABC的顶点都在正三角形的格点上,将△ABC绕点O逆时针旋转120°得到△A′B′C′.
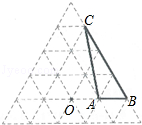
(1)在网格中画出旋转后的△A′B′C′;
(2)求AB边旋转时扫过的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
类别
时间t(小时)
人数
A
t≤0.5
5
B
0.5<t≤1
20
C
1<t≤1.5
a
D
1.5<t≤2
30
E
t>2
10
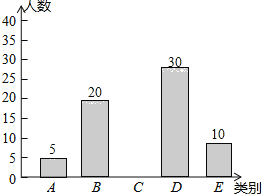
请根据图表信息解答下列问题:
(1)a= ;
(2)补全条形统计图;
(3)小王说:“我每天的锻炼时间是调查所得数据的中位数”,问小王每天进行体育锻炼的时间在什么范围内?
(4)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.
相关试题

