【题目】已知四边形ABCD中,EF分别是AB、AD边上的点,DE与CF交于点G.
(1)如图1,若四边形ABCD是正方形,且DE⊥CF,求证:DE=CF;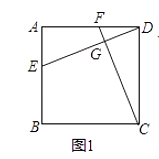
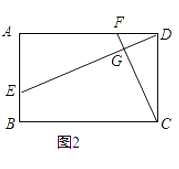
(2)如图2,若四边形ABCD是矩形,且DE⊥CF,求证: ![]() =
= ![]() ;
;
(3)如图3,若四边形ABCD是平行四边形,当∠B=∠EGF时,第(2)问的结论是否成立?若成立给予证明;若不成立,请说明理由.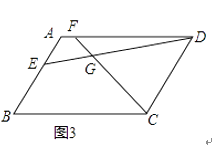
参考答案:
【答案】
(1)证明:∵四边形ABCD是正方形,
∴∠A=∠ADC=90°,AD=DC,
∴∠ADE+∠AED=90°,
∵DE⊥CF,
∴∠ADE+∠CFD=90°,
∴∠AED=∠CFD,
∴△ADE≌△DCF,
∴DE=CF
(2)证明:∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,
∵DE⊥CF,
∴∠ADE+∠CFD=90°,∠DCF+∠CFD=90°,
∴∠ADE=∠DCF,
∴△ADE∽△DCF,
∴ ![]() =
= ![]()
(3)解:当∠B=∠EGF时, ![]() =
= ![]() 成立,
成立,
证明:如图3,在AD的延长线上取点M,使CM=CF,
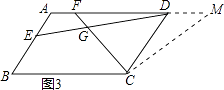
则∠CMF=∠CFM,
∵AB∥CD,
∴∠A=∠CDM,
∵AD∥BC,
∴∠B+∠A=180°,
∵∠B=∠EGF,
∴∠EGF+∠A=180°,
∴∠AED=∠CFM=∠CMF,
∴△ADE∽△DCM,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]()
【解析】(1)依据正方形的性质可得到∠A=∠ADC=90°,AD=DC,然后再依据同角的余角相等可证明∠AED=∠CFD,最后,在依据AAS证明△ADE≌△DCF,最后,利用全等三角形对应边相等进行证明即可;
(2)依据矩形的性质可得到∠A=∠ADC=90°,然后再依据同角的余角相等可证明∠ADE=∠DCF,接下来,利用两对角相等的三角形相似得到三角形ADE与三角形DCF相似,最后,利用相似三角形对应边成比例进行证明即可;
(3)在AD的延长线上取点M,使CM=CF,先证明△ADE∽△DCM,然后再利用相似三角形对应边成比例进行证明即可.
【考点精析】利用相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走50m到达C点,测得点B在点C的北偏东60°方向,如图2,求出这段河的宽(结果精确到1m,备用数据
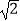 ≈1.41,
≈1.41, 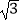 ≈1.73).
≈1.73).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,MN是⊙O的切线,B为切点,BC是⊙O的弦且∠CBN=45°,过C的直线与⊙O,MN分别交于A,D两点,过C作CE⊥BD于点E.、
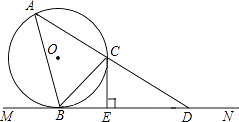
(1)求证:CE是⊙O的切线;
(2)若∠D=30°,BD=4,求⊙O的半径r. -
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆拥有客房90间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元)
200
240
270
300
y(间)
90
70
55
40
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房,宾馆每日需支出60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入﹣当日支出) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在
 中,
中, .在边
.在边 上取一点
上取一点 ,以
,以 为顶点、
为顶点、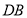 为一条边作
为一条边作 ,点
,点 在
在 的延长线上,
的延长线上, .
.(1)如图(1),当点
 在边
在边 上时,请说明①
上时,请说明① ;②
;② 成立的理由.
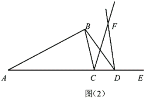
成立的理由.(2)如图(2),当点
 在
在 的延长线上时,试判断
的延长线上时,试判断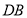 与
与 是否相等?
是否相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣
 x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.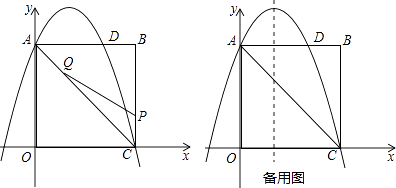
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣ x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
相关试题

