【题目】某宾馆拥有客房90间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元) | 200 | 240 | 270 | 300 |
y(间) | 90 | 70 | 55 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房,宾馆每日需支出60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入﹣当日支出)
参考答案:
【答案】
(1)解:设y=kx+b,
将(200,90)、(240,70)代入,得:
![]() ,
,
解得: 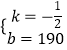 ,
,
∴y=﹣ ![]() x+190
x+190
(2)解:设宾馆当日利润为W,
则W=(x﹣100)y﹣60(90﹣y)
=(x﹣100)(﹣ ![]() x+190)﹣60[90﹣(﹣
x+190)﹣60[90﹣(﹣ ![]() x+190)]
x+190)]
=﹣ ![]() x2+210x﹣13000
x2+210x﹣13000
=﹣ ![]() (x﹣210)2+9050,
(x﹣210)2+9050,
∴当x=210时,W最大=9050,
答:当房价为210元时,宾馆当日利润最大,最大利润为9050元
【解析】(1)设一次函数的解析式为y=kx+b,然后选取表格中两组对应值代入得到关于k、b的方程组,从而可求得k、b的值;
(2)根据“总利润=每间客房的利润×入住客房数量-每间空置客房的支出×空置客房数量”列出函数解析式,然后利用配方法将函数关系式变形为顶点式的性质,从而可得到函数的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分15分,成绩均记为整数分),并按测试成绩(单位:分)分成四类:A类(12≤m≤15),B类(9≤m≤11),C类(6≤m≤8),D类(m≤5)绘制出以下两幅不完整的统计图,请根据图中信息解答下列问题:
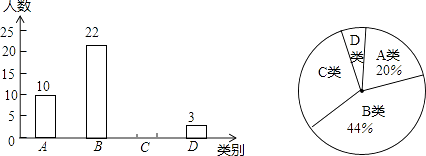
(1)本次抽取样本容量为 , 扇形统计图中A类所对的圆心角是度;
(2)请补全统计图;
(3)若该校九年级男生有300名,请估计该校九年级男生“引体向上”项目成绩为C类的有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走50m到达C点,测得点B在点C的北偏东60°方向,如图2,求出这段河的宽(结果精确到1m,备用数据
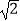 ≈1.41,
≈1.41, 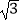 ≈1.73).
≈1.73).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,MN是⊙O的切线,B为切点,BC是⊙O的弦且∠CBN=45°,过C的直线与⊙O,MN分别交于A,D两点,过C作CE⊥BD于点E.、
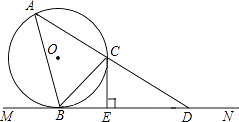
(1)求证:CE是⊙O的切线;
(2)若∠D=30°,BD=4,求⊙O的半径r. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD中,EF分别是AB、AD边上的点,DE与CF交于点G.
(1)如图1,若四边形ABCD是正方形,且DE⊥CF,求证:DE=CF;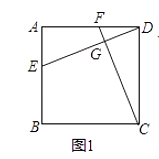
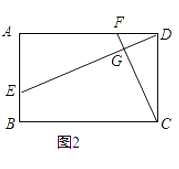
(2)如图2,若四边形ABCD是矩形,且DE⊥CF,求证: =
= 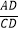 ;
;
(3)如图3,若四边形ABCD是平行四边形,当∠B=∠EGF时,第(2)问的结论是否成立?若成立给予证明;若不成立,请说明理由.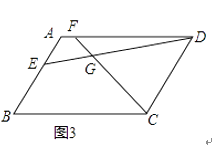
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在
 中,
中, .在边
.在边 上取一点
上取一点 ,以
,以 为顶点、
为顶点、 为一条边作
为一条边作 ,点
,点 在
在 的延长线上,
的延长线上, .
.(1)如图(1),当点
 在边
在边 上时,请说明①
上时,请说明① ;②
;② 成立的理由.
成立的理由.(2)如图(2),当点
 在
在 的延长线上时,试判断
的延长线上时,试判断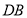 与
与 是否相等?
是否相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

相关试题

