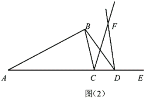
【题目】已知在![]() 中,
中,![]() .在边
.在边![]() 上取一点
上取一点![]() ,以
,以![]() 为顶点、
为顶点、![]() 为一条边作
为一条边作![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上,![]() .
.
(1)如图(1),当点![]() 在边
在边![]() 上时,请说明①
上时,请说明①![]() ;②
;②![]() 成立的理由.
成立的理由.
(2)如图(2),当点![]() 在
在![]() 的延长线上时,试判断
的延长线上时,试判断![]() 与
与![]() 是否相等?
是否相等?

参考答案:
【答案】(1)见解析;(2)![]()
【解析】
(1)①直接利用三角形的外角性质,即可得到;
②过D作![]() 交
交![]() 于点
于点![]() ,由等腰三角形的性质,平行线的性质和等边对等角,得到
,由等腰三角形的性质,平行线的性质和等边对等角,得到![]() ,
,![]() ,然后证明三角形全等,即可得到结论成立;
,然后证明三角形全等,即可得到结论成立;
(2)连接BF,根据题意,可证得![]() ,则B、C、D、F四点共圆,即可证明结论成立.
,则B、C、D、F四点共圆,即可证明结论成立.
解:(1)①∵![]() ,
,
即![]() ,
,
∵![]() ,
,
∴![]() ;
;
②过D作![]() 交
交![]() 于点
于点![]() ,
,

∴![]() ,
,![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,
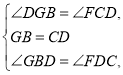
∴![]()
∴![]() ;
;
(2)证明:如图:连接BF,

由(1)可知,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴B、C、D、F四点共圆,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,MN是⊙O的切线,B为切点,BC是⊙O的弦且∠CBN=45°,过C的直线与⊙O,MN分别交于A,D两点,过C作CE⊥BD于点E.、
(1)求证:CE是⊙O的切线;
(2)若∠D=30°,BD=4,求⊙O的半径r. -
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆拥有客房90间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元)
200
240
270
300
y(间)
90
70
55
40
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房,宾馆每日需支出60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入﹣当日支出) -
科目: 来源: 题型:
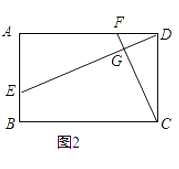
查看答案和解析>>【题目】已知四边形ABCD中,EF分别是AB、AD边上的点,DE与CF交于点G.
(1)如图1,若四边形ABCD是正方形,且DE⊥CF,求证:DE=CF;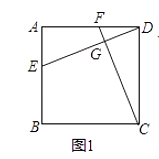
(2)如图2,若四边形ABCD是矩形,且DE⊥CF,求证: =
= 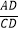 ;
;
(3)如图3,若四边形ABCD是平行四边形,当∠B=∠EGF时,第(2)问的结论是否成立?若成立给予证明;若不成立,请说明理由.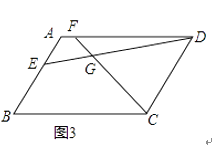
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣
 x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.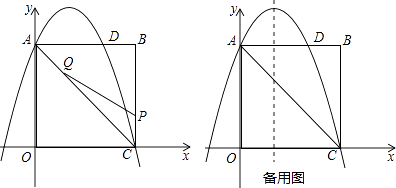
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣ x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①所示是一个长为
 ,宽为
,宽为 的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.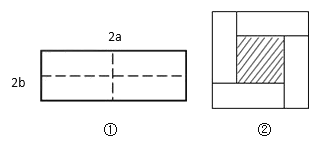
(1)图②中的阴影部分的正方形的边长等于 .(用含
 ,
, 的代数式表示)
的代数式表示)(2)请用两种不同的方法列代数式表示图②中阴影部分的面积:
方法①: .
方法②: .
(3)观察图②,直接写出
 、
、 、
、 这三个代数式之间的等量关系.
这三个代数式之间的等量关系.(4)根据(3)题中的等量关系,若
 ,
, ,求图②中阴影部分的面积.
,求图②中阴影部分的面积.
相关试题

