【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

参考答案:
【答案】(1)反比例函数解析式为y=﹣![]() ,一次函数解析式为y=﹣2x﹣4;(2)4.
,一次函数解析式为y=﹣2x﹣4;(2)4.
【解析】
试题分析:(1)将点A坐标代入反比例函数求出m的值,从而得到点A的坐标以及反比例函数解析式,再将点B坐标代入反比例函数求出n的值,从而得到点B的坐标,然后利用待定系数法求一次函数解析式求解;
(2)设AB与x轴相交于点C,根据一次函数解析式求出点C的坐标,从而得到点OC的长度,再根据S△AOB=S△AOC+S△BOC列式计算即可得解.
试题解析:(1)将A(﹣3,m+8)代入反比例函数y=![]() 得,
得,
![]() =m+8,
=m+8,
解得m=﹣6,
m+8=﹣6+8=2,
所以,点A的坐标为(﹣3,2),
反比例函数解析式为y=﹣![]() ,
,
将点B(n,﹣6)代入y=﹣![]() 得,﹣
得,﹣![]() =﹣6,
=﹣6,
解得n=1,
所以,点B的坐标为(1,﹣6),
将点A(﹣3,2),B(1,﹣6)代入y=kx+b得,
![]() ,
,
解得![]() ,
,
所以,一次函数解析式为y=﹣2x﹣4;
(2)设AB与x轴相交于点C,
令﹣2x﹣4=0解得x=﹣2,
所以,点C的坐标为(﹣2,0),
所以,OC=2,
S△AOB=S△AOC+S△BOC,
=![]() ×2×3+
×2×3+![]() ×2×1,
×2×1,
=3+1,
=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:﹣3x3+12x2﹣12x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年11月9日是第29个“消防宣传日”.某校举行“安全小能手”消防安全知识竞赛,有50位同学参加比赛,比赛结束后根据每个学生的最后得分计算出平均数、中位数、众数和方差,如果去掉一个最高分和一个最低分,则一定不发生变化的是( ).
A.平均数B.中位数C.众数D.方差
-
科目: 来源: 题型:
查看答案和解析>>【题目】SARS﹣CoV﹣2是一种新型冠状病毒,其病毒颗粒呈多形性,其中球形病毒的最大直径为0.000 000 14米,这一直径用科学记数法表示为( ).
A.1.4×10-7米B.1.4×10-8米C.14×10-7米D.14×10-8米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
(1)当0<t<5时,用含t的式子表示BP,AQ
(2)当t=2时,求PQ的值;
(3)当PQ= AB时,求t的值.
AB时,求t的值.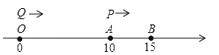
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:

为了丰富社会实践活动,引导学生科学探究,学校组织七年级同学走进中国科技馆,亲近科学,感受科技魅力.来到科技馆大厅,同学们就被大厅里会“跳舞”的“小球矩阵”吸引住了(如图1).白色小球全部由计算机精准控制,每一只小球可以“悬浮”在大厅上空的不同位置,演绎着曲线、曲面、平面、文字和三维图案等各种动态造型.
已知每个小球分别由独立的电机控制.图2,图3分别是9个小球可构成的两个造型,在每个造型中,相邻小球的高度差均为a.为了使小球从造型一(如图2)变到造型二(如图3),控制电机使造型一中的②,③,④,⑥,⑦,⑧号小球同时运动,②,③,④号小球向下运动,运动速度均为3米/秒;⑥,⑦,⑧号小球向上运动,运动速度均为2米/秒,当每个小球到达造型二的相应位置时就停止运动.已知⑦号小球比②号小球晚 秒到达相应位置,问②号小球运动了多少米?
秒到达相应位置,问②号小球运动了多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴交于A、B两点,若m>1,且点A在点B的左侧,OA:OB=1:3
(1)试确定抛物线的解析式;
(2)直线y=kx﹣3与抛物线交于M、N两点,若△AMN的内心在x轴上,求k的值.
(3)设(2)中抛物线与y轴的交点为C,过点C作直线l∥x轴,将抛物线在y轴左侧的部分沿直线l翻折,抛物线的其余部分保持不变,得到一个新图象,请你结合新图象回答:当直线y=
 x+b与新图象只有一个公共点P(x0,y0)且y0≤7时,求b的取值范围.
x+b与新图象只有一个公共点P(x0,y0)且y0≤7时,求b的取值范围.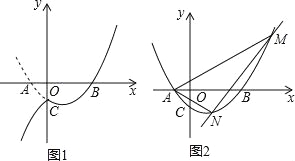
相关试题

