【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣ ![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.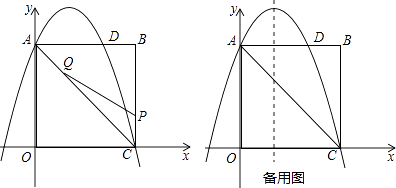
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣ ![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:将A、C两点坐标代入抛物线,得
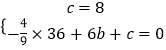 ,
,
解得: ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+8
x+8
(2)解:①∵OA=8,OC=6,
∴AC= ![]() =10,
=10,
过点Q作QE⊥BC与E点,
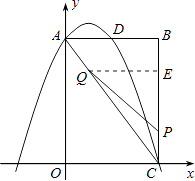
则sin∠ACB= ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴QE= ![]() (10﹣m),
(10﹣m),
∴S= ![]() CPQE=
CPQE= ![]() m×
m× ![]() (10﹣m)=﹣
(10﹣m)=﹣ ![]() m2+3m;
m2+3m;
②∵S= ![]() CPQE=
CPQE= ![]() m×
m× ![]() (10﹣m)=﹣
(10﹣m)=﹣ ![]() m2+3m=﹣
m2+3m=﹣ ![]() (m﹣5)2+
(m﹣5)2+ ![]() ,
,
∴当m=5时,S取最大值;
在抛物线对称轴l上存在点F,使△FDQ为直角三角形,
∵抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+8的对称轴为x=
x+8的对称轴为x= ![]() ,
,
D的坐标为(3,8),Q(34),
当∠FDQ=90°时,F1( ![]() ,8),
,8),
当∠FQD=90°时,则F2( ![]() ,4),
,4),
当∠DFQ=90°时,设F( ![]() ,n),
,n),
则FD2+FQ2=DQ2,
即 ![]() +(8﹣n)2+
+(8﹣n)2+ ![]() +(n﹣4)2=16,
+(n﹣4)2=16,
解得:n=6± ![]() ,
,
∴F3( ![]() ,6+
,6+ ![]() ),F4(
),F4( ![]() ,6﹣
,6﹣ ![]() ),
),
满足条件的点F共有四个,坐标分别为
F1( ![]() ,8),F2(
,8),F2( ![]() ,4),F3(
,4),F3( ![]() ,6+
,6+ ![]() ),F4(
),F4( ![]() ,6﹣
,6﹣ ![]() ).
).
【解析】(1)将A、C两点坐标代入抛物线的解析式可得到关于b、c的方程组,接下来,解方程求得b、c的值,从而可求得抛物线的解析式;
(2)①先依据勾股定理求得AC的长,从而可表示CQ的长,然后过点Q作QE⊥BC与E点,依据锐角三角函数的定义可求得QE的长,然后依据三角形的面积公式可得到S与m的函数关系式;②先依据函数关系式求得当S最大值是m的值,从而可确定出点Q的坐标,然后再求得抛物线的对称轴从而得到点F的横坐标,然后再分为∠FDQ=90°,∠FQD=90°、∠DFQ=90°三种情况求得点F的纵坐标即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD中,EF分别是AB、AD边上的点,DE与CF交于点G.
(1)如图1,若四边形ABCD是正方形,且DE⊥CF,求证:DE=CF;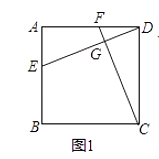
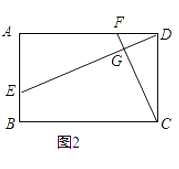
(2)如图2,若四边形ABCD是矩形,且DE⊥CF,求证: =
= 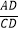 ;
;
(3)如图3,若四边形ABCD是平行四边形,当∠B=∠EGF时,第(2)问的结论是否成立?若成立给予证明;若不成立,请说明理由.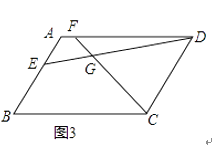
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在
 中,
中, .在边
.在边 上取一点
上取一点 ,以
,以 为顶点、
为顶点、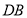 为一条边作
为一条边作 ,点
,点 在
在 的延长线上,
的延长线上, .
.(1)如图(1),当点
 在边
在边 上时,请说明①
上时,请说明① ;②
;② 成立的理由.
成立的理由.(2)如图(2),当点
 在
在 的延长线上时,试判断
的延长线上时,试判断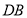 与
与 是否相等?
是否相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

-
科目: 来源: 题型:
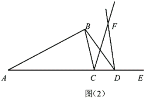
查看答案和解析>>【题目】如图①所示是一个长为
 ,宽为
,宽为 的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.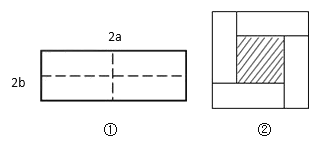
(1)图②中的阴影部分的正方形的边长等于 .(用含
 ,
, 的代数式表示)
的代数式表示)(2)请用两种不同的方法列代数式表示图②中阴影部分的面积:
方法①: .
方法②: .
(3)观察图②,直接写出
 、
、 、
、 这三个代数式之间的等量关系.
这三个代数式之间的等量关系.(4)根据(3)题中的等量关系,若
 ,
, ,求图②中阴影部分的面积.
,求图②中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步中途改为步行,到达图书馆恰好用30min.小东骑自行车以300m/min的速度直接回家,两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示
(1)家与图书馆之间的路程为多少m,小玲步行的速度为多少m/min;
(2)求小东离家的路程y关于x的函数解析式,并写出自变量的取值范围;
(3)求两人相遇的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】星期天,小明骑车从家出发到某景区游玩,他先匀速骑了一段上坡路,休息一会儿,又匀速骑了一段下坡路后到达目的地,下图表示的是他骑车行驶的距离
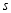 (千米)与行驶时间
(千米)与行驶时间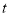 (分)之间的变化情况.根据图象,回答下列问题:
(分)之间的变化情况.根据图象,回答下列问题: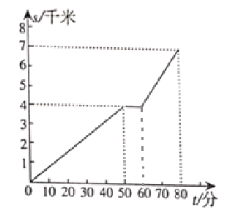
(1)小明家到景区的距离为 千米;
(2)小明途中休息了 分;
(3)返回途中,若小明的上下坡速度保持不变,并且中途不再休息,求小明从景区到家所用的时间.
相关试题

