【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+4分别交x轴、y轴于点B、点C,直线CD交x轴于点A,点D的坐标为(﹣
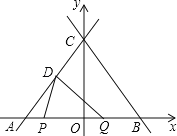
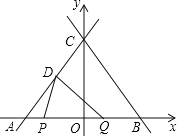
x+4分别交x轴、y轴于点B、点C,直线CD交x轴于点A,点D的坐标为(﹣![]() ,2),点P在线段AB上以每秒1个单位的速度从点A运动到点B,点Q在线段AB上以每秒2个单位的速度从点B运动到点A,P、Q两点同时出发,设点P的运动时间为t(秒),△DPQ的面积为S(S>0).
,2),点P在线段AB上以每秒1个单位的速度从点A运动到点B,点Q在线段AB上以每秒2个单位的速度从点B运动到点A,P、Q两点同时出发,设点P的运动时间为t(秒),△DPQ的面积为S(S>0).
(1)BQ的长为 (用含t的代数式表示);
(2)求点A的坐标;
(3)求S与t之间的函数关系式.
参考答案:
【答案】(1)2t;(2)点A的坐标为(﹣3,0);(3)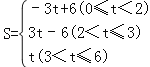
【解析】解:(1)∵点Q在线段AB上以每秒2个单位的速度从点B运动到点A,
∴BQ=2t.
故答案为:2t.
(2)∵直线y=﹣![]() x+4分别交x轴、y轴于点B、点C,
x+4分别交x轴、y轴于点B、点C,
∴当x=0时,y=4,
∴点C的坐标为(0,4).
当y=0时,x=3,
∴点B的坐标为(3,0).
设直线CD所对应的函数表达式为y=kx+b(k≠0),
将C(0,4)、D(﹣![]() ,2)代入y=kx+b中,
,2)代入y=kx+b中,
得: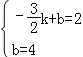 ,解得:
,解得:![]() ,
,
∴直线CD所对应的函数表达式为y=![]() x+4.
x+4.
∵直线CD交x轴于点A,
当y=0时,x=﹣3,
∴点A的坐标为(﹣3,0).
(3)∵A(﹣3,0),B(3,0),点P在线段AB上以每秒1个单位的速度从点A运动到点B,点Q在线段AB上以每秒2个单位的速度从点B运动到点A,
∴AB=3﹣(﹣3)=6,
∴当t=2时,P、Q重合,当t=3时点Q到达A点,当t=6时,点P到达B点.
当0≤t<2时,S=![]() PQyD=
PQyD=![]() ×2×(6﹣t﹣2t)=﹣3t+6;
×2×(6﹣t﹣2t)=﹣3t+6;
当2<t≤3时,S=![]() PQyD=
PQyD=![]() ×2×(t+2t﹣6)=3t﹣6;
×2×(t+2t﹣6)=3t﹣6;
当3<t≤6时,S=![]() APyD=
APyD=![]() ×2×t=t.
×2×t=t.
综上可知: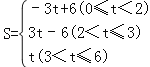 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是面积为
 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 (结果保留根号).
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 (结果保留根号).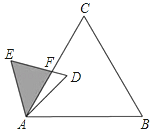
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,北部湾海面上,一艘解放军军舰在基地A的正东方向且距A地60海里的B处训练,突然接到基地命令,要该舰前往C岛,接送一名病危的渔民到基地医院救治.已知C岛在A的北偏东30°方向,且在B的北偏西60°方向,军舰从B处出发,平均每小时行驶30海里,需要多少时间才能把患病渔民送到基地医院.(精确到0.1小时,
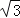 ≈1.7)
≈1.7)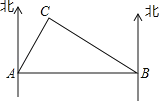
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
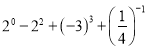
(2)
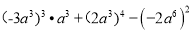
(3)

(4)
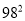 (用乘法公式计算)
(用乘法公式计算) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 1的相反数是﹣1 B. 1的倒数是﹣1
C. 1的立方根是±1 D. ﹣1是无理数
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程9x2﹣6x+k=0有两个不相等的实根,则k的范围是( )
A.k<1
B.k>1
C.k≤1
D.k≥1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:x2+16x﹣k是完全平方式,则k=______.
相关试题

