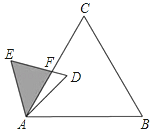
【题目】如图,已知△ABC是面积为![]() 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 (结果保留根号).
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于 (结果保留根号).
参考答案:
【答案】![]() .
.
【解析】
试题分析:根据相似三角形面积比等于相似比的平方求得三角形ADE的面积,再根据求出其边长,可根据三角函数得出三角形面积.
解:∵△ABC∽△ADE,AB=2AD,
∴![]() =
=![]() ,
,
∵AB=2AD,S△ABC=![]() ,
,
∴S△ADE=![]() ,
,
如图,在△EAF中,过点F作FH⊥AE交AE于H,
∵∠EAF=∠BAD=45°,∠AEF=60°,
∴∠AFH=45°,∠EFH=30°,
∴AH=HF,
设AH=HF=x,则EH=xtan30°=![]() x.
x.
又∵S△ADE=![]() ,
,
作CM⊥AB交AB于M,
∵△ABC是面积为![]() 的等边三角形,
的等边三角形,
∴![]() ×AB×CM=
×AB×CM=![]() ,
,
∠BCM=30°,
设AB=2k,BM=k,CM=![]() k,
k,
∴k=1,AB=2,
∴AE=![]() AB=1,
AB=1,
∴x+![]() x=1,
x=1,
解得x=![]() =
=![]() .
.
∴S△AEF=![]() ×1×
×1×![]() =
=![]() .
.
故答案为:![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知第一个正方体纸盒的棱长为6cm,第二个正方体纸盒的体积比第一个纸盒的体积大127cm3,求第二个纸盒的棱长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2x2-8y2=__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正n边形的每个内角为156°,则这个正n边形的边数是( )
A.13
B.14
C.15
D.16 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,北部湾海面上,一艘解放军军舰在基地A的正东方向且距A地60海里的B处训练,突然接到基地命令,要该舰前往C岛,接送一名病危的渔民到基地医院救治.已知C岛在A的北偏东30°方向,且在B的北偏西60°方向,军舰从B处出发,平均每小时行驶30海里,需要多少时间才能把患病渔民送到基地医院.(精确到0.1小时,
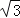 ≈1.7)
≈1.7)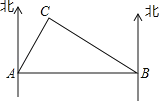
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
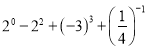
(2)
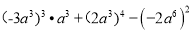
(3)

(4)
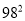 (用乘法公式计算)
(用乘法公式计算) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣
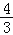 x+4分别交x轴、y轴于点B、点C,直线CD交x轴于点A,点D的坐标为(﹣
x+4分别交x轴、y轴于点B、点C,直线CD交x轴于点A,点D的坐标为(﹣ ,2),点P在线段AB上以每秒1个单位的速度从点A运动到点B,点Q在线段AB上以每秒2个单位的速度从点B运动到点A,P、Q两点同时出发,设点P的运动时间为t(秒),△DPQ的面积为S(S>0).
,2),点P在线段AB上以每秒1个单位的速度从点A运动到点B,点Q在线段AB上以每秒2个单位的速度从点B运动到点A,P、Q两点同时出发,设点P的运动时间为t(秒),△DPQ的面积为S(S>0).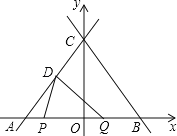
(1)BQ的长为 (用含t的代数式表示);
(2)求点A的坐标;
(3)求S与t之间的函数关系式.
相关试题

