【题目】已知:射线![]() 在
在![]() 的内部,
的内部,![]() ,
,![]() ,
,![]() 平分
平分![]() .
.
(1)如图,若点![]() ,
,![]() ,
,![]() 在同一条直线上,
在同一条直线上,![]() 是
是![]() 内部的一条射线,请根据题意补全图形,并求
内部的一条射线,请根据题意补全图形,并求![]() 的度数;
的度数;
(2)若![]() ,直接写出
,直接写出![]() 的度数(用含
的度数(用含![]() 的代数式表示).
的代数式表示).

参考答案:
【答案】(1)图详见解析,![]() ;(2)当射线
;(2)当射线![]() 在
在![]() 的内部时,
的内部时,![]() ; 当射线
; 当射线![]() 在
在![]() 的外部时,
的外部时,![]() .
.
【解析】
(1)作出∠AOD的平分线OE,根据∠AOC:∠BOC=8:1求出∠BOC=20°,依据∠COD=2∠COB得∠COD=40°,从而可求∠AOD=120°,根据OE平分∠AOD得∠DOE=60°,从而可求出![]() 的度数;
的度数;
(2)分两种情况考虑:当射线![]() 在
在![]() 的内部时,
的内部时,![]() ;当射线
;当射线![]() 在
在![]() 的外部时,
的外部时,![]() .
.
(1)补全图形,如图所示:
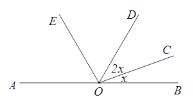
∵点![]() ,
,![]() ,
,![]() 在同一条直线上,
在同一条直线上,
∴![]() (平角的定义) .
(平角的定义) .
∵![]() ,
,
∴![]() ,
, ![]() .
.
∵![]() ,
,
∴![]() .
.
∴
∵![]() 平分
平分![]() ,
,
∴![]() (角平分线的定义).
(角平分线的定义).
∴![]()
(2)①当射线![]() 在
在![]() 的内部时,如图,
的内部时,如图,
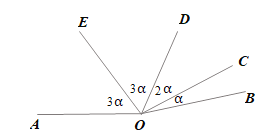
∵![]() ,
,![]()
∴∠AOC=8α,
∵![]()
∴![]()
∴∠AOD=∠AOC-∠COD=6α,
∵![]() 平分
平分![]()
∴∠DOE=![]() ∠AOD=3α,
∠AOD=3α,
∴∠COE=∠COD+∠DOE=2α+3α=5α;
当射线![]() 在
在![]() 的外部时,如图,
的外部时,如图,
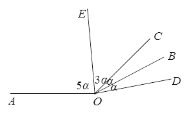
∵![]() ,
,![]()
∴∠AOC=8α,
∵![]()
∴![]() ,∠BOD=α
,∠BOD=α
∴∠AOD=∠AOC+∠COD=10α,
∵![]() 平分
平分![]()
∴∠DOE=![]() ∠AOD=5α,
∠AOD=5α,
∴∠COE=∠DOE -∠COD =5α-2α=3α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线
 与x轴交于A、B两点,与y轴交于点C.直线
与x轴交于A、B两点,与y轴交于点C.直线 经过抛物线与坐标轴的两个交点B和C。
经过抛物线与坐标轴的两个交点B和C。(1)求直线BC的解析式;
(2)点D是线段BC上的一个动点(与两个端点均不重合),过点D引y轴的平行线PD交抛物线于点P,设抛物线的对称轴为直线
 ,如果以点P为圆心的⊙P与直线BC相切,请用点P的横坐标x表示⊙P的半径R。
,如果以点P为圆心的⊙P与直线BC相切,请用点P的横坐标x表示⊙P的半径R。(3)在(2)的基础上判断⊙P与直线
 的位置关系。
的位置关系。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求平行四边形ACDE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂制作甲、乙两种环保包装盒,已知同样用6m材料制成甲盒的个数比制成乙盒的个数少2个,且制成一个甲盒比制成一个乙盒需要多用20%的材料.
(1)求制作每个甲盒、乙盒各用多少米材料?
(2)如果制作甲、乙两种包装盒共3000个,且甲盒的数量不少于乙盒数量的2倍,那么请写出所需要材料的总长度l(m)与甲盒数量n(个)之间的函数关系式,并求出最少需要多少米材料?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ACE中,CA=CE,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.
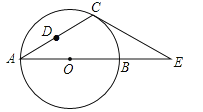
(1)试说明CE是⊙O的切线;
(2)若△ACE中AE边上的高为h,试用含h的代数式表示⊙O的直径AB;
(3)设点D是线段AC上任意一点(不含端点),连接OD,当
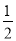 CD+OD的最小值为6时,求⊙O的直径AB的长.
CD+OD的最小值为6时,求⊙O的直径AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】现代营养学家用身体质量指数来判断人体的健康状态,这个指数等于人体质量(千克)与人体身高(米)平方得商,一个健康的人身体质量指数在20~25之间,身体质量指数低于18,属于不健康的瘦;身体质量指数高于30,属于不健康的胖。
(1)若一个人的质量为w千克,身高h米,用含字母w,h的代数式表示他的身体质量指数
(2)王先生的身高是1.75米,质量68千克,请判断他的身体是否健康。
-
科目: 来源: 题型:
查看答案和解析>>【题目】五一期间,甲、乙两人分别骑自行车和摩托车从
 地出发前往
地出发前往 地郊游,并以各自的速度匀速行驶,到达目的地停止,途中乙休息了一段时间,然后又继续赶路.甲、乙两人各自行驶的路程
地郊游,并以各自的速度匀速行驶,到达目的地停止,途中乙休息了一段时间,然后又继续赶路.甲、乙两人各自行驶的路程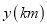 与所用时间
与所用时间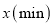 之间的函数图象如图所示.
之间的函数图象如图所示.
(1)甲骑自行车的速度是_____
 .
.(2)求乙休息后所行的路程
 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围.
的取值范围.(3)为了保证及时联络,甲、乙两人在第一次相遇时约定此后两人之间的路程不超过
 .甲、乙两人是否符合约定,并说明理由.
.甲、乙两人是否符合约定,并说明理由.
相关试题

