【题目】如图,在△ACE中,CA=CE,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.
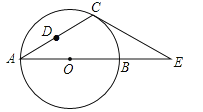
(1)试说明CE是⊙O的切线;
(2)若△ACE中AE边上的高为h,试用含h的代数式表示⊙O的直径AB;
(3)设点D是线段AC上任意一点(不含端点),连接OD,当![]() CD+OD的最小值为6时,求⊙O的直径AB的长.
CD+OD的最小值为6时,求⊙O的直径AB的长.
参考答案:
【答案】(1)证明见试题解析;(2)AB= ![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)连接OC,如图1,要证CE是⊙O的切线,只需证∠OCE=90°即可;
(2)过点C作CH⊥AB于H,连接OC,如图2,在Rt△OHC中运用三角函数即可;
(3)作OF平分∠AOC,交⊙O于F,连接AF、CF、DF,如图3,先证四边形AOCF是菱形,由对称性可得DF=DO.过点D作DH⊥OC于H,易得DH=![]() DC,从而有
DC,从而有![]() CD+OD=DH+FD.根据两点之间线段最短可得:当F、D、H三点共线时,DH+FD(即
CD+OD=DH+FD.根据两点之间线段最短可得:当F、D、H三点共线时,DH+FD(即![]() CD+OD)最小,然后在Rt△OHF中运用三角函数即可解决问题.
CD+OD)最小,然后在Rt△OHF中运用三角函数即可解决问题.
试题解析:(1)连接OC,如图1,∵CA=CE,∠CAE=30°,∴∠E=∠CAE=30°,∠COE=2∠A=60°,∴∠OCE=90°,∴CE是⊙O的切线;
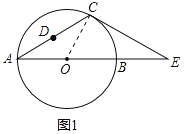
(2)过点C作CH⊥AB于H,连接OC,如图2,由题可得CH=h,在Rt△OHC中,CH=OCsin∠COH,∴h=OCsin60°=![]() OC,∴OC=
OC,∴OC=![]() =
= ![]() ,∴AB=2OC=
,∴AB=2OC= ![]() ;
;
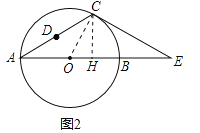
(3)作OF平分∠AOC,交⊙O于F,连接AF、CF、DF,如图3,则∠AOF=∠COF=![]() ∠AOC=
∠AOC=![]() (180°﹣60°)=60°,∵OA=OF=OC,∴△AOF、△COF是等边三角形,∴AF=AO=OC=FC,∴四边形AOCF是菱形,∴根据对称性可得DF=DO,过点D作DH⊥OC于H,∵OA=OC,∴∠OCA=∠OAC=30°,∴DH=DCsin∠DCH=DCsin30°=
(180°﹣60°)=60°,∵OA=OF=OC,∴△AOF、△COF是等边三角形,∴AF=AO=OC=FC,∴四边形AOCF是菱形,∴根据对称性可得DF=DO,过点D作DH⊥OC于H,∵OA=OC,∴∠OCA=∠OAC=30°,∴DH=DCsin∠DCH=DCsin30°=![]() DC,∴
DC,∴![]() CD+OD=DH+FD.根据两点之间线段最短可得:当F、D、H三点共线时,DH+FD(即
CD+OD=DH+FD.根据两点之间线段最短可得:当F、D、H三点共线时,DH+FD(即![]() CD+OD)最小,此时FH=OFsin∠FOH=
CD+OD)最小,此时FH=OFsin∠FOH=![]() OF=6,则OF=
OF=6,则OF=![]() ,AB=2OF=
,AB=2OF=![]() ,∴当
,∴当![]() CD+OD的最小值为6时,⊙O的直径AB的长为
CD+OD的最小值为6时,⊙O的直径AB的长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求平行四边形ACDE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂制作甲、乙两种环保包装盒,已知同样用6m材料制成甲盒的个数比制成乙盒的个数少2个,且制成一个甲盒比制成一个乙盒需要多用20%的材料.
(1)求制作每个甲盒、乙盒各用多少米材料?
(2)如果制作甲、乙两种包装盒共3000个,且甲盒的数量不少于乙盒数量的2倍,那么请写出所需要材料的总长度l(m)与甲盒数量n(个)之间的函数关系式,并求出最少需要多少米材料?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:射线
 在
在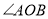 的内部,
的内部, ,
, ,
, 平分
平分 .
.(1)如图,若点
 ,
, ,
, 在同一条直线上,
在同一条直线上, 是
是 内部的一条射线,请根据题意补全图形,并求
内部的一条射线,请根据题意补全图形,并求 的度数;
的度数;(2)若
 ,直接写出
,直接写出 的度数(用含
的度数(用含 的代数式表示).
的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】现代营养学家用身体质量指数来判断人体的健康状态,这个指数等于人体质量(千克)与人体身高(米)平方得商,一个健康的人身体质量指数在20~25之间,身体质量指数低于18,属于不健康的瘦;身体质量指数高于30,属于不健康的胖。
(1)若一个人的质量为w千克,身高h米,用含字母w,h的代数式表示他的身体质量指数
(2)王先生的身高是1.75米,质量68千克,请判断他的身体是否健康。
-
科目: 来源: 题型:
查看答案和解析>>【题目】五一期间,甲、乙两人分别骑自行车和摩托车从
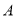 地出发前往
地出发前往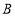 地郊游,并以各自的速度匀速行驶,到达目的地停止,途中乙休息了一段时间,然后又继续赶路.甲、乙两人各自行驶的路程
地郊游,并以各自的速度匀速行驶,到达目的地停止,途中乙休息了一段时间,然后又继续赶路.甲、乙两人各自行驶的路程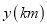 与所用时间
与所用时间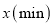 之间的函数图象如图所示.
之间的函数图象如图所示.
(1)甲骑自行车的速度是_____
 .
.(2)求乙休息后所行的路程
 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围.
的取值范围.(3)为了保证及时联络,甲、乙两人在第一次相遇时约定此后两人之间的路程不超过
 .甲、乙两人是否符合约定,并说明理由.
.甲、乙两人是否符合约定,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(问题情境)在综合实践课上,同学们以“图形的平移”为主题开展数学活动,如图①,先将一张长为4,宽为3的矩形纸片沿对角线剪开,拼成如图所示的四边形
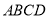 ,
, ,
, ,则拼得的四边形
,则拼得的四边形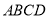 的周长是_____.
的周长是_____.
(操作发现)将图①中的
 沿着射线
沿着射线 方向平移,连结
方向平移,连结 、
、 、
、 、
、 ,如图②.当
,如图②.当 的平移距离是
的平移距离是 的长度时,求四边形
的长度时,求四边形 的周长.
的周长. (操作探究)将图②中的
 继续沿着射线
继续沿着射线 方向平移,其它条件不变,当四边形
方向平移,其它条件不变,当四边形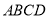 是菱形时,将四边形
是菱形时,将四边形 沿对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
沿对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
相关试题

