【题目】如图1,抛物线![]() 与x轴交于A、B两点,与y轴交于点C.直线
与x轴交于A、B两点,与y轴交于点C.直线![]() 经过抛物线与坐标轴的两个交点B和C。
经过抛物线与坐标轴的两个交点B和C。
(1)求直线BC的解析式;
(2)点D是线段BC上的一个动点(与两个端点均不重合),过点D引y轴的平行线PD交抛物线于点P,设抛物线的对称轴为直线![]() ,如果以点P为圆心的⊙P与直线BC相切,请用点P的横坐标x表示⊙P的半径R。
,如果以点P为圆心的⊙P与直线BC相切,请用点P的横坐标x表示⊙P的半径R。
(3)在(2)的基础上判断⊙P与直线![]() 的位置关系。
的位置关系。

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,⊙P与抛物线对称轴x=1相离,当
时,⊙P与抛物线对称轴x=1相离,当![]() 时,⊙P与抛物线对称轴x=1相切,当
时,⊙P与抛物线对称轴x=1相切,当![]() 时,⊙P与抛物线对称轴x=1相交.
时,⊙P与抛物线对称轴x=1相交.
【解析】试题分析: ![]() 分别令
分别令![]() 求得
求得![]() 三点的坐标,即可用待定系数法求出直线
三点的坐标,即可用待定系数法求出直线![]() 的解析式.
的解析式.
![]() 设点D坐标为(
设点D坐标为(![]() )(0<x<4),P(
)(0<x<4),P(![]() ),进而表示出
),进而表示出![]() ,
,
作![]() 于点M,延长PD交x轴于点H,先用勾股定理求出
于点M,延长PD交x轴于点H,先用勾股定理求出![]() 的长,用三角函数即可表示出
的长,用三角函数即可表示出![]() 的半径
的半径![]()
![]() 分类讨论即可.
分类讨论即可.
试题解析:(1)令![]() 中y=0,得
中y=0,得![]() ,
,
![]() ,
,
解得: ![]() ,
,
![]() 易知
易知![]()
将B、C坐标分别代入![]() ,得
,得![]() 解得:
解得: 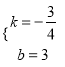 ,
,
∴直线BC的解析式为: ![]() ;
;
(2)由题可设点D坐标为(![]() )(0<x<4),P(
)(0<x<4),P(![]() ),
),
∴PD=![]() =
= ![]() ,(∵
,(∵![]() ),
),
如图1,作![]() 于点M,延长PD交x轴于点H,则
于点M,延长PD交x轴于点H,则![]()
![]() ,∴
,∴![]() ,
,
∴![]() 的半径
的半径![]()
![]() ,即
,即![]() ;
;
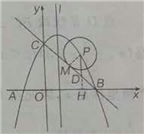
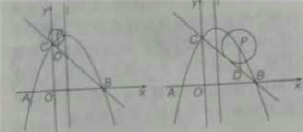
图1 图2 图3
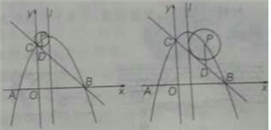
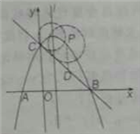
图4 图5 图6
(3)抛物线的对称轴![]() 是直线x=1,分类讨论:
是直线x=1,分类讨论:
①当![]() 与直线x=1在左侧相切(0<x<1),则
与直线x=1在左侧相切(0<x<1),则![]() ,
,
整理得: ![]() ,解得:
,解得: ![]() ,∵0<x<1,∴
,∵0<x<1,∴![]() ;
;
②当![]() 与直线
与直线![]() 在右侧相切(1<x<4),则
在右侧相切(1<x<4),则![]() ,整理得:
,整理得: ![]() ,解得:
,解得: ![]() ,∵1<x<4,∴
,∵1<x<4,∴![]() ;
;
综上所述,当![]() 或
或![]() 时,
时, ![]() 与抛物线对称轴
与抛物线对称轴![]() 相离,如图2和图3所示;
相离,如图2和图3所示;
当![]() 或
或![]() 时,
时, ![]() 与抛物线对称轴
与抛物线对称轴![]() 相切,如图4和图5所示;
相切,如图4和图5所示;
当![]() 时,
时, ![]() 与抛物线对称轴
与抛物线对称轴![]() 相交,如图6所示.
相交,如图6所示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】认真阅读材料,然后回答问题:我们初中学习了多项式的运算法则,相应的我们可以计算出多项式的展开式,如:(a+b)1=a+b,
(a+b)2=a2+2ab+b2,(a+b)3=a3+3a2b+3ab2+b3,…下面我们依次对(a+b)n展开式的各项系数进一步研究发现,当n取正整数是可以单独列成表中的形式:

上面的多项式展开系数表称为“杨辉三角形”;仔细观察“杨辉三角形”,用你发现的规律回答下列问题:(1)
 展开式中共有多少项?
展开式中共有多少项?(2)请写出多项式
 的展开式?
的展开式? -
科目: 来源: 题型:
查看答案和解析>>【题目】对连续的偶数2,4,6,8,…排成如图的形式.若将图中的十字框上下左右移动,框住的五个数之和能等于2020吗?若能,请写出这五个数中位置在最中间的数;若不能,请说明理由.你的答案是:____________________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求平行四边形ACDE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂制作甲、乙两种环保包装盒,已知同样用6m材料制成甲盒的个数比制成乙盒的个数少2个,且制成一个甲盒比制成一个乙盒需要多用20%的材料.
(1)求制作每个甲盒、乙盒各用多少米材料?
(2)如果制作甲、乙两种包装盒共3000个,且甲盒的数量不少于乙盒数量的2倍,那么请写出所需要材料的总长度l(m)与甲盒数量n(个)之间的函数关系式,并求出最少需要多少米材料?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:射线
 在
在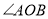 的内部,
的内部, ,
, ,
, 平分
平分 .
.(1)如图,若点
 ,
, ,
, 在同一条直线上,
在同一条直线上, 是
是 内部的一条射线,请根据题意补全图形,并求
内部的一条射线,请根据题意补全图形,并求 的度数;
的度数;(2)若
 ,直接写出
,直接写出 的度数(用含
的度数(用含 的代数式表示).
的代数式表示).
相关试题

