【题目】综合题。
(1)如图1,已知AD=BC,AC=BD.求证:△ADB≌△BCA. 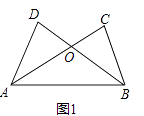
(2)如图2,已知AB是⊙O的一条直径,延长AB至点C,使AC=3BC,CD与⊙O相切于点D,若CD= ![]() ,求⊙O的半径.
,求⊙O的半径. 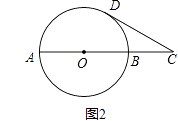
参考答案:
【答案】
(1)证明:在△ADB与△BCA中,

∴△ADB≌△BCA(SSS)
(2)解:连接OD,
∵CD与⊙O相切,
∴OD⊥CD,
∴∠ODC=90°,
∵AC=3BC,AB=2OB,
∴OB=BC,
∴OB= ![]() OC
OC
又OB=OD,
∴OD= ![]() OC
OC
在Rt△ODC,
cos∠DOC= ![]() =
= ![]() ,
,
∴∠DOC=60°,
∴∠AOD=120°
在Rt△POC中,
由勾股定理可知:OD2+DC2=OC2,
∵CD= ![]() ,
,
∴OD2+3=4OD2,
∴OD=1
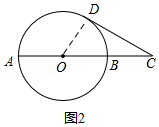
【解析】(1)根据全等三角形的判定即求证;(2)连接OD,利用AC=3BC可知OB= ![]() OC,在Rt△ODC中,cos∠DOC=
OC,在Rt△ODC中,cos∠DOC= ![]() =
= ![]() ,从而可知∠DOC=60°,∠AOD=120°,在Rt△POC中,利用勾股定理即可求出OD的长度.
,从而可知∠DOC=60°,∠AOD=120°,在Rt△POC中,利用勾股定理即可求出OD的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)先化简,再求值:a(a﹣2b)+(a+b)2 , 其中a=﹣1,b=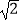 .
.
(2)解方程: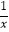 =
= 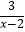 .
. -
科目: 来源: 题型:
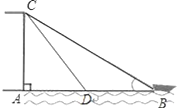
查看答案和解析>>【题目】已知:如图,有人在岸上点C的地方,用绳子拉船靠岸,开始时,绳长CB=10米,CA⊥AB,且CA=6米,拉动绳子将船从点B沿BA方向行驶到点D后,绳长CD=6
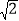 米.
米.(1)试判定△ACD的形状,并说明理由;
(2)求船体移动距离BD的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为E.
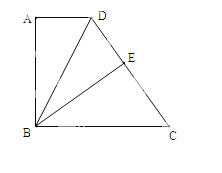
(1)求证:DA=DE;
(2)若AD=2,BC=6,求AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t)
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5
5≤x<6
10
20%
6≤x<7
12%
7≤x<8
3
6%
8≤x<9
2
4%
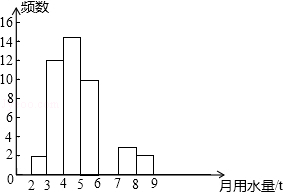
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B、与y轴交于点A,与反比例函数y=
 的图象在第二象限交于C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于C,CE⊥x轴,垂足为点E,tan∠ABO=  ,OB=4,OE=2.
,OB=4,OE=2.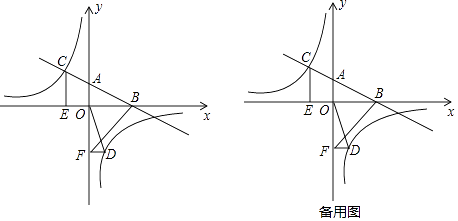
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限内的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO , 求点D的坐标.
(3)若动点D在反比例函数图象的第四象限上运动,当线段DC与线段DB之差达到最大时,求点D的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 经过点
经过点 ,
, .
.
(1)求直线
 的解析式;
的解析式;(2)若直线
 与直线
与直线 相交于点
相交于点 ,求点
,求点 的坐标;
的坐标;(3)根据图象,直接写出关于
 的不等式
的不等式 的解集.
的解集.
相关试题

