【题目】已知直线![]() 经过点
经过点![]() ,
,![]() .
.

(1)求直线![]() 的解析式;
的解析式;
(2)若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)根据图象,直接写出关于![]() 的不等式
的不等式![]() 的解集.
的解集.
参考答案:
【答案】(1)直线AB的解析式为y=-x+5;(2)点C的坐标为(3,2);(3)由图可知,x≥3时,2x-4≥kx+b.
【解析】
试题分析:(1)利用待定系数法把点A(5,0),B(1,4)代入y=kx+b可得关于k、b得方程组,再解方程组即可;(2)联立两个函数解析式,再解方程组即可;(3)根据C点坐标可直接得到答案.
试题解析:(1)∵直线y=kx+b经过点A(5,0),B(1,4),
∴![]() ,
,
解得![]() ,
,
∴直线AB的解析式为:y=-x+5;
∵若直线y=2x-4与直线AB相交于点C,
∴![]() .
.
解得![]() ,
,
∴点C(3,2);
(3)根据图象可得x≥3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:(1)
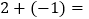 _______;(2)
_______;(2)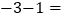 ________;
________;(3)
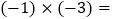 _______;(4)
_______;(4)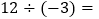 _______;
_______;(5)
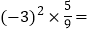 ________;(6)
________;(6)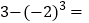 ________.
________. -
科目: 来源: 题型:
查看答案和解析>>【题目】探究规律,完成相关题目.
老师说:“我定义了一种新的运算,叫(加乘)运算.”
然后老师写出了一些按照(加乘)运算的运算法则进行运算的算式:
(+5)(+2)=+7;(-3)(-5)=+8;
(-3)(+4)=-7; (+5)(-6)=-11;
0(+8)=8;(-6)0=6.
小明看了这些算式后说:“我知道老师定义的(加乘)运算的运算法则了.”
聪明的你也明白了吗?
(1)归纳(加乘)运算的运算法则:
两数进行(加乘)运算时,运算法则是什么.
特别地,0和任何数进行(加乘)运算,或任何数和0进行(加乘)运算运算法则是什么.
(2)计算:
①(
 )[
)[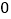 (
( )].(括号的作用与它在有理数运算中的作用一致)
)].(括号的作用与它在有理数运算中的作用一致) ② 若(
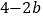 )(
)(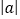
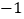 )
)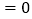 .求
.求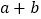 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a、b、c为常数,a≠0)经过点A(﹣1,0),B(5,﹣6),C(6,0).
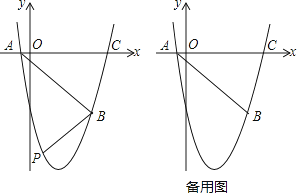
(1)求抛物线的解析式;
(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上 -
科目: 来源: 题型:
查看答案和解析>>【题目】某水果批发市场苹果的价格如下表:
购买苹果
(千克)不超过20千克的部分
超过20千克但不超出40千克的部分
超出40千克的部分
每千克的价格
6元
5元
4元
(1)小明第一次购买苹果10千克,需要付费多少元;
小明第二次购买苹果
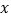 千克(
千克(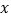 超过20千克但不超过40千克),需要付费多少元(用含
超过20千克但不超过40千克),需要付费多少元(用含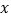 的式子表示);
的式子表示);(2)小强分两次共购买100千克,第二次购买的数量多于第一次购买的数量,且第一次购买的数量为
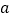 千克,请问小强两次购买苹果共需要付费多少元?(用含
千克,请问小强两次购买苹果共需要付费多少元?(用含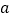 的式子表示);
的式子表示); -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②c>0;③a+c<b;④b2﹣4ac>0,其中正确的个数是( )
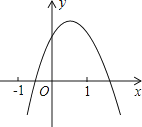
A.1
B.2
C.3
D.4
相关试题

