【题目】如图,在四边形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为E.
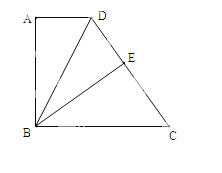
(1)求证:DA=DE;
(2)若AD=2,BC=6,求AB.
参考答案:
【答案】(1)详见解析;(2)AB=![]() .
.
【解析】
(1)利用已知条件证明△ABD≌△EBD,根据确定三角形的对应边相等得到DA=DE;
(2)由△ABD≌△EBD,得到AD=DE=4,从而求得CE=6,在Rt△BCE中,利用勾股定理求得BE2=BC2-CE2=8,即可解答.
(1)证明:∵AB⊥AD,BE⊥DC
∴∠A=∠BED=90°
∵BC=CD
∴∠DBC=∠BDC
∵AD∥BC
∴∠DBC=∠ADB
∴∠BDC=∠ADB
∴△ABD≌△EBD
∴DA=DE
(2)解:∵△ABD≌△EBD
∴AD=DE=2
∵BC=CD=6
∴CE=4
在Rt△BCE中,BE2= BC2-CE2= 62-42 =20
∴BE=![]()
∴AB=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的长度构造一组正方形(如下图),再分别依次从左到右取2个,3个,4个,5个正方形拼成如下长方形并记为①,②,③,④,相应长方形的周长如下表所示:
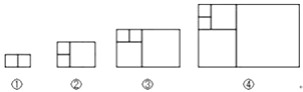

若按此规律继续作长方形,则序号为⑧的长方形周长是( )
A. 288 B. 178 C. 28 D. 110
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)先化简,再求值:a(a﹣2b)+(a+b)2 , 其中a=﹣1,b=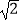 .
.
(2)解方程: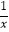 =
= 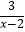 .
. -
科目: 来源: 题型:
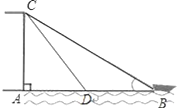
查看答案和解析>>【题目】已知:如图,有人在岸上点C的地方,用绳子拉船靠岸,开始时,绳长CB=10米,CA⊥AB,且CA=6米,拉动绳子将船从点B沿BA方向行驶到点D后,绳长CD=6
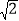 米.
米.(1)试判定△ACD的形状,并说明理由;
(2)求船体移动距离BD的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)如图1,已知AD=BC,AC=BD.求证:△ADB≌△BCA.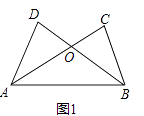
(2)如图2,已知AB是⊙O的一条直径,延长AB至点C,使AC=3BC,CD与⊙O相切于点D,若CD=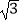 ,求⊙O的半径.
,求⊙O的半径. 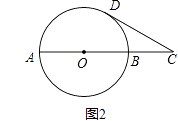
-
科目: 来源: 题型:
查看答案和解析>>【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t)
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5
5≤x<6
10
20%
6≤x<7
12%
7≤x<8
3
6%
8≤x<9
2
4%
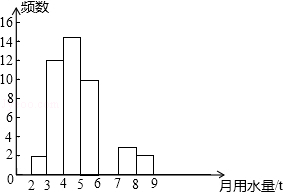
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B、与y轴交于点A,与反比例函数y=
 的图象在第二象限交于C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于C,CE⊥x轴,垂足为点E,tan∠ABO=  ,OB=4,OE=2.
,OB=4,OE=2.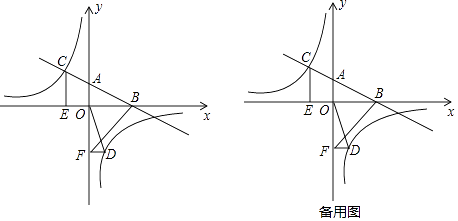
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限内的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO , 求点D的坐标.
(3)若动点D在反比例函数图象的第四象限上运动,当线段DC与线段DB之差达到最大时,求点D的坐标.
相关试题

