【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B、与y轴交于点A,与反比例函数y= ![]() 的图象在第二象限交于C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于C,CE⊥x轴,垂足为点E,tan∠ABO= ![]() ,OB=4,OE=2.
,OB=4,OE=2.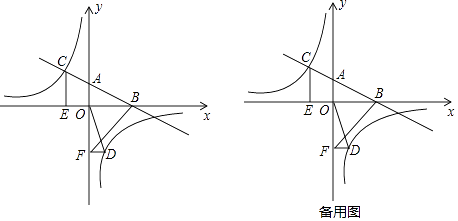
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限内的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO , 求点D的坐标.
(3)若动点D在反比例函数图象的第四象限上运动,当线段DC与线段DB之差达到最大时,求点D的坐标.
参考答案:
【答案】
(1)
解:∵tan∠ABO= ![]() ,
,
∴ ![]() =
= ![]() ,且OB=4,
,且OB=4,
∴OA=2,
∵CE⊥x轴,即CE∥AO,
∴△AOB∽△CEB,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得CE=3,
,解得CE=3,
∴C(﹣2,3),
∴m=﹣2×3=﹣6,
∴反比例函数解析式为y=﹣ ![]()
(2)
解:设D(x,﹣ ![]() ),
),
∵D在第四象限,
∴DF=x,OF= ![]() ,
,
∴S△DFO= ![]() DFOF=
DFOF= ![]() x×
x× ![]() =3,
=3,
由(1)可知OA=2,
∴AF=x+ ![]() ,
,
∴S△BAF= ![]() AFOB=
AFOB= ![]() (x+
(x+ ![]() )×4=2(x+
)×4=2(x+ ![]() ),
),
∵S△BAF=4S△DFO,
∴2(x+ ![]() )=4×3,解得x=3+
)=4×3,解得x=3+ ![]() 或x=3﹣
或x=3﹣ ![]() ,
,
当x=3+ ![]() 时,﹣
时,﹣ ![]() 的值为3﹣
的值为3﹣ ![]() ,
,
当x=3﹣ ![]() 时,﹣
时,﹣ ![]() 的值为3+
的值为3+ ![]() ,
,
∵D在第四象限,
∴x=3﹣ ![]() 不合题意,舍去,
不合题意,舍去,
∴D(3+ ![]() ,3﹣
,3﹣ ![]() )
)
(3)
解:∵D在第四象限,
∴在△BCD中,由三角形三边关系可知CD﹣CB≤BC,即当B、C、D三点共线时,其差最大,
设直线AB解析式为y=kx+b,
由题意可得 ![]() ,解得
,解得 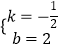 ,
,
∴直线AB解析式为y=﹣ ![]() x+2,
x+2,
联立直线AB和反比例函数解析式可得 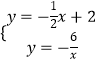 ,解得
,解得 ![]() 或
或 ![]() (舍去),
(舍去),
∴D(6,﹣1),
即当线段DC与线段DB之差达到最大时求点D的坐标为(6,﹣1)
【解析】(1)由条件可求得OA,由△AOB∽△CEB可求得CE,则可求得C点坐标,代入反比例函数解析式可求得m的值,可求得反比例函数解析式;(2)设出D的坐标,从而可分别表示出△BAF和△DFO的面积,由条件可列出方程,从而可求得D点坐标;(3)在△BCD中,由三角形三边关系可知CD﹣CB≤BC,当B、C、D三点共线时,其差最大,联立直线BC与反比例函数解析式可求得D点坐标.
【考点精析】解答此题的关键在于理解反比例函数的性质的相关知识,掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大,以及对三角形三边关系的理解,了解三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为E.
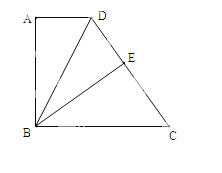
(1)求证:DA=DE;
(2)若AD=2,BC=6,求AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)如图1,已知AD=BC,AC=BD.求证:△ADB≌△BCA.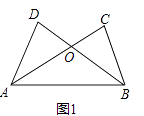
(2)如图2,已知AB是⊙O的一条直径,延长AB至点C,使AC=3BC,CD与⊙O相切于点D,若CD=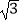 ,求⊙O的半径.
,求⊙O的半径. 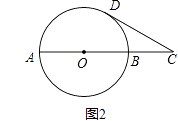
-
科目: 来源: 题型:
查看答案和解析>>【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t)
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5
5≤x<6
10
20%
6≤x<7
12%
7≤x<8
3
6%
8≤x<9
2
4%
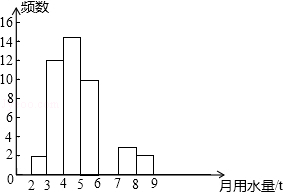
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 经过点
经过点 ,
, .
.
(1)求直线
 的解析式;
的解析式;(2)若直线
 与直线
与直线 相交于点
相交于点 ,求点
,求点 的坐标;
的坐标;(3)根据图象,直接写出关于
 的不等式
的不等式 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进
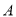 、
、 两种新型节能台灯共
两种新型节能台灯共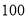 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:
(
 )若商场预计进货款为
)若商场预计进货款为 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?(
 )若商场规定
)若商场规定 型台灯的进货数量不超过
型台灯的进货数量不超过 型台灯数量的
型台灯数量的 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】某股民上周五购进某公司股票500股,每股30元.(星期六、星期日封盘,关闭交易)下表是本周内每日该股票比前一天的涨跌情况(单位:元)

星期一,星期二被墨水污染,只知道星期一比上周五上涨10%,星期二比星期一下跌10%.根据以上信息,请回答:
(1)星期三收盘时,每股是多少元?
(2)本周内每股最高价是多少元?最低价是多少元?
(3)已知该股民购进股票时付了1.5‰的手续费,卖出时还要付成交额1.5‰的手续费和1‰的交易税.如果他在星期五收盘时全部卖出该股票,他是赚钱还是亏本?赚或亏了多少钱?
相关试题

