【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=4,∠BCD=120°,求四边形AODE的面积.

参考答案:
【答案】(1)详见解析;(2)矩形AODE面积为![]()
【解析】
(1)根据菱形的性质得出AC⊥BD,再根据平行四边形的判定定理得四边形AODE为平行四边形,由矩形的判定定理得出四边形AODE是矩形;
(2)证明△ABC是等边三角形,得出OA=![]() ×4=2,由勾股定理得出OB=2
×4=2,由勾股定理得出OB=2![]() ,由菱形的性质得出OD=OB=2
,由菱形的性质得出OD=OB=2![]() ,即可求出四边形AODE的面积.
,即可求出四边形AODE的面积.
(1)证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴平行四边形AODE是矩形,
故四边形AODE是矩形;
(2)解:∵∠BCD=120°,AB∥CD,
∴∠ABC=180°-120°=60°,
∵AB=BC,
∴△ABC是等边三角形,
∴OA=![]() ×4=2,
×4=2,
∵在菱形ABCD中,AC⊥BD
∴由勾股定理OB=![]() =2
=2![]() ,
,
∵四边形ABCD是菱形,
∴OD=OB=2![]() ,
,
∴四边形AODE的面积=OAOD=2![]() =4
=4![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE.
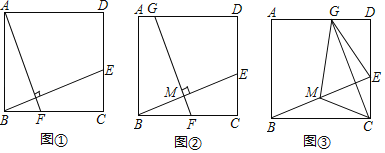
(感知)如图①,过点A作AF⊥BE交BC于点F.易证△ABF≌△BCE.(不需要证明)
(探究)如图②,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(1)求证:BE=FG.
(2)连结CM,若CM=1,则FG的长为 .
(应用)如图③,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
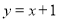 的图象与反比例函数
的图象与反比例函数 (
( 为常数,且
为常数,且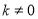 )的图象都经过点A(m,2).
)的图象都经过点A(m,2).
(1)求点A的坐标及反比例函数的表达式;
(2)设一次函数
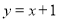 的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.
的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, ;那么
;那么 与
与 平行吗?试说明理由.
平行吗?试说明理由.
请将下面的推理过程补充完整.
解:
 ,理由如下:
,理由如下: (已知)
(已知) (平角的定义)
(平角的定义) ( )
( )
 ( )
( ) (两直线平行,同位角相等)
(两直线平行,同位角相等) (已知)
(已知) ( )
( ) (内错角相等,两直线平行)
(内错角相等,两直线平行) -
科目: 来源: 题型:
查看答案和解析>>【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:

(1)图中自变量是______,因变量是______;
(2)小明家到学校的路程是 米;
(3)小明在书店停留了 分钟;
(4)本次上学途中,小明一共行驶了 米,一共用了 分钟;
(5)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
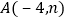 ,
, 是一次函数
是一次函数 的图象和反比例函数
的图象和反比例函数 的图象的两个交点.
的图象的两个交点.(1)求一次函数、反比例函数的关系式;
(2)求△AOB的面积
(3) 当自变量x满足什么条件时,
 >
> .(直接写出答案)
.(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,点
,点 是直线
是直线 上一点(不与
上一点(不与 重合),以
重合),以 为一边在
为一边在 的右侧作
的右侧作 ,使
,使 ,
, ,连接
,连接 .
.
(1)如图1,当点
 在线段
在线段 上时.如果
上时.如果 ,则
,则 __________.
__________.(2)设
 ,
, .
.①如图2,当点
 在线段
在线段 上移动时,
上移动时,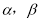 之间有怎样的数量关系?请说明理由.
之间有怎样的数量关系?请说明理由.②当点
 在直线
在直线 上移动时,
上移动时,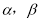 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.
相关试题

