【题目】在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE.
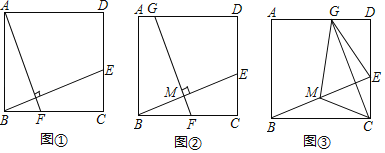
(感知)如图①,过点A作AF⊥BE交BC于点F.易证△ABF≌△BCE.(不需要证明)
(探究)如图②,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(1)求证:BE=FG.
(2)连结CM,若CM=1,则FG的长为 .
(应用)如图③,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为 .
参考答案:
【答案】(1)证明见解析;(2)2,9.
【解析】感知:利用同角的余角相等判断出∠BAF=∠CBE,即可得出结论;
探究:(1)判断出PG=BC,同感知的方法判断出△PGF≌CBE,即可得出结论;
(2)利用直角三角形的斜边的中线是斜边的一半,
应用:借助感知得出结论和直角三角形斜边的中线是斜边的一半即可得出结论.
感知:∵四边形ABCD是正方形,
∴AB=BC,∠BCE=∠ABC=90°,
∴∠ABE+∠CBE=90°,
∵AF⊥BE,
∴∠ABE+∠BAF=90°,
∴∠BAF=∠CBE,
在△ABF和△BCE中,
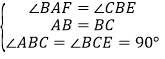 ,
,
∴△ABF≌△BCE(ASA);
探究:(1)如图②,
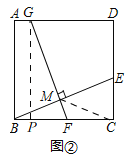
过点G作GP⊥BC于P,
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠ABC=90°,
∴四边形ABPG是矩形,
∴PG=AB,∴PG=BC,
同感知的方法得,∠PGF=∠CBE,
在△PGF和△CBE中,
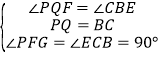 ,
,
∴△PGF≌△CBE(ASA),
∴BE=FG;
(2)由(1)知,FG=BE,
连接CM,
∵∠BCE=90°,点M是BE的中点,
∴BE=2CM=2,
∴FG=2,
故答案为:2.
应用:同探究(2)得,BE=2ME=2CM=6,
∴ME=3,
同探究(1)得,CG=BE=6,
∵BE⊥CG,
∴S四边形CEGM=![]() CG×ME=
CG×ME=![]() ×6×3=9,
×6×3=9,
故答案为:9.
-
科目: 来源: 题型:
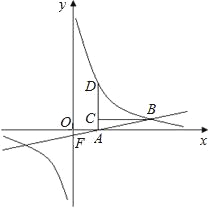
查看答案和解析>>【题目】如图,点D在双曲线上,AD垂直x轴,垂足为A,点C在AD上,CB平行于x轴交双曲线于点B,直线AB与y轴交于点F,已知AC:AD=1:3,点C的坐标为(3,2).
(1)求该双曲线的解析式;
(2)求△OFA的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于D1, ∠ABD1与∠ACD1的角平分线交于点D2,依次类推,∠ABD4与∠ACD4 的角平分线交于点D5,则∠BD5C的度数是( )

A. 56°;B. 60°;C. 68°;D. 94°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 是
是 的中点,
的中点, ,
, ,
, 平分
平分 ,下列结论:①
,下列结论:① ;②
;② ;③
;③ ;④
;④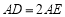 ,四个结论中成立的是__________.
,四个结论中成立的是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
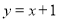 的图象与反比例函数
的图象与反比例函数 (
( 为常数,且
为常数,且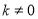 )的图象都经过点A(m,2).
)的图象都经过点A(m,2).
(1)求点A的坐标及反比例函数的表达式;
(2)设一次函数
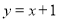 的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.
的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, ;那么
;那么 与
与 平行吗?试说明理由.
平行吗?试说明理由.
请将下面的推理过程补充完整.
解:
 ,理由如下:
,理由如下: (已知)
(已知) (平角的定义)
(平角的定义) ( )
( )
 ( )
( ) (两直线平行,同位角相等)
(两直线平行,同位角相等) (已知)
(已知) ( )
( ) (内错角相等,两直线平行)
(内错角相等,两直线平行) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=4,∠BCD=120°,求四边形AODE的面积.

相关试题

