【题目】如图,已知![]() ,
,![]() 是一次函数
是一次函数![]() 的图象和反比例函数
的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求一次函数、反比例函数的关系式;
(2)求△AOB的面积
(3) 当自变量x满足什么条件时,![]() >
>![]() .(直接写出答案)
.(直接写出答案)

参考答案:
【答案】(1)![]() ,
,![]() ;(2)△AOB的面积为6;(3)x<-4或0<x<2.
;(2)△AOB的面积为6;(3)x<-4或0<x<2.
【解析】
(1)把B (2,-4)代入反比例函数y2=![]() 得出m的值,然后求出n的值,再把A(-4,2)B(2,-4)代入一次函数的解析式y1=kx+b,运用待定系数法求其解析式;
得出m的值,然后求出n的值,再把A(-4,2)B(2,-4)代入一次函数的解析式y1=kx+b,运用待定系数法求其解析式;
(2)由y1=-x-2即可求得点C的坐标,把三角形AOB的面积看成是三角形AOC和三角形OCB的面积之和进行计算即可求得.
(3)根据图象,分别观察交点的那一侧能够使一次函数的值大于反比例函数的值,从而求得x的取值范围.
(1)∵B(2,-4)在反比例函数y2=![]() 的图象上,
的图象上,
∴m=-8.
∴反比例函数的解析式为y2=-![]() .
.
∵点A(-4,n)在y2=-![]() 上,
上,
∴n=2.
∴A(-4,2).
∵y1=kx+b经过A(-4,2),B(2,-4),
∴![]() ,
,
解得:![]() ,
,
∴一次函数的解析式为y1=-x-2.
(2)∴C是直线AB与x轴的交点,
∴当y=0时,x=-2.
∴点C(-2,0).
∴OC=2.
∴S△AOB=S△ACO+S△BCO=![]() ×2×2+
×2×2+![]() ×2×4=6.
×2×4=6.
(3)由图象,得,
当x的取值范围是x<-4或0<x<2时,y1>y2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, ;那么
;那么 与
与 平行吗?试说明理由.
平行吗?试说明理由.
请将下面的推理过程补充完整.
解:
 ,理由如下:
,理由如下: (已知)
(已知) (平角的定义)
(平角的定义) ( )
( )
 ( )
( ) (两直线平行,同位角相等)
(两直线平行,同位角相等) (已知)
(已知) ( )
( ) (内错角相等,两直线平行)
(内错角相等,两直线平行) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=4,∠BCD=120°,求四边形AODE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:

(1)图中自变量是______,因变量是______;
(2)小明家到学校的路程是 米;
(3)小明在书店停留了 分钟;
(4)本次上学途中,小明一共行驶了 米,一共用了 分钟;
(5)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,点
,点 是直线
是直线 上一点(不与
上一点(不与 重合),以
重合),以 为一边在
为一边在 的右侧作
的右侧作 ,使
,使 ,
, ,连接
,连接 .
.
(1)如图1,当点
 在线段
在线段 上时.如果
上时.如果 ,则
,则 __________.
__________.(2)设
 ,
, .
.①如图2,当点
 在线段
在线段 上移动时,
上移动时,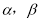 之间有怎样的数量关系?请说明理由.
之间有怎样的数量关系?请说明理由.②当点
 在直线
在直线 上移动时,
上移动时,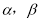 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是反比例函数
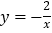 在第二象限内图象上一点,点B是反比例函
在第二象限内图象上一点,点B是反比例函 数在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,求△AOB的面积.
数在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,求△AOB的面积.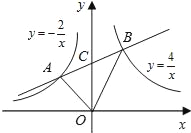
-
科目: 来源: 题型:
查看答案和解析>>【题目】火车匀速通过隧道时,火车在隧道内的长度
 (米)与火车行驶时间
(米)与火车行驶时间 (秒)之间的关系用图象描述如图所示,有下列结论:
(秒)之间的关系用图象描述如图所示,有下列结论:①火车的长度为120米;
②火车的速度为30米/秒;
③火车整体都在隧道内的时间为25秒;
④隧道长度为750米.
其中正确的结论是_____.(把你认为正确结论的序号都填上)

相关试题

