【题目】某校![]() 名学生参加植树活动,要求每人植
名学生参加植树活动,要求每人植![]() 棵,活动结束后随机抽查了
棵,活动结束后随机抽查了![]() 名学生每人的植树量,并分为四种类型,
名学生每人的植树量,并分为四种类型,![]() :
:![]() 棵;
棵;![]() ;
;![]() 棵;
棵;![]() :
:![]() 棵,
棵,![]() :
:![]() 棵。将各类的人绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误。
棵。将各类的人绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误。
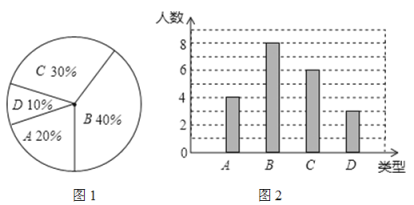
回答下列问题:
(1)写出条形图中存在的错误,并说明理由.
(2)写出这![]() 名学生每人植树量的众数、中位数.
名学生每人植树量的众数、中位数.
(3)在求这![]() 名学生每人植树量的平均数.
名学生每人植树量的平均数.
(4)估计这![]() 名学生共植树多少棵.
名学生共植树多少棵.
参考答案:
【答案】(1)D;(2)5,5;(3)这![]() 名学生每人植树量的平均数5.3;(4)估计这260名学生共植树1378棵.
名学生每人植树量的平均数5.3;(4)估计这260名学生共植树1378棵.
【解析】
(1)利用总人数乘对应的百分比求解即可;
(2)根据众数、中位数的定义即可直接求解;
(3)直接列式即可求得调查的20人的平均数;
(4)用平均数乘以总人数260即可.
(1)D错误,理由:20×10%=2≠3;
(2)由题意可知,植树5棵人数最多,故众数为5,
共有20人植树,其中位数是第10、11人植树数量的平均数,
即![]() (5+5)=5,故中位数为5;
(5+5)=5,故中位数为5;
(3)这![]() 名学生每人植树量的平均数(4×4+5×8+6×6+7×2)÷20=5.3,
名学生每人植树量的平均数(4×4+5×8+6×6+7×2)÷20=5.3,
(4)估计这260名学生共植树5.3×260=1378(棵).
答:估计这260名学生共植树1378棵
-
科目: 来源: 题型:
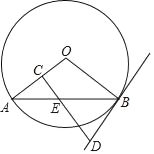
查看答案和解析>>【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正常情况下,一个人在运动时所能承受的每分钟心跳的最高次数y(次/分)是这个人年龄x(岁)的一次函数。
(1)根据图中信息,求在正常情况下,y关于x的函数关系式;
(2)若一位63岁的人在跑步,医生在途中给他测得10秒心跳为26次,问:他是否有危险?为什么?

-
科目: 来源: 题型:
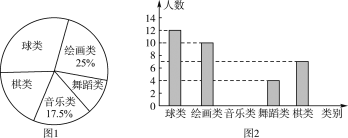
查看答案和解析>>【题目】为了解某校落实新课改精神的情况,现以该校九年级二班的同学参加课外活动的情况为样本,对其参加“球类”“绘画类”“舞蹈类”“音乐类”“棋类”活动的情况进行调查统计,并绘制了如图所示的统计图.
(1)参加音乐类活动的学生人数为____人,参加球类活动的人数的百分比为____;
(2)请把条形统计图补充完整;
(3)若该校学生共600人,那么参加棋类活动的大约有多少人?
(4)该班参加舞蹈类活动的4位同学中,有1位男生(用E表示)和3位女生(分别用F,G,H表示),现准备从中选取两名同学组成舞伴,请用列表或画树状图的方法求恰好选中一男一女的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣x+2与反比例函数y=
 (k≠0)的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
(k≠0)的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.(1)求a,b的值及反比例函数的解析式;
(2)若点P在直线y=﹣x+2上,且S△ACP=S△BDP,请求出此时点P的坐标;
(3)在x轴正半轴上是否存在点M,使得△MAB为等腰三角形?若存在,请直接写出M点的坐标;若不存在,说明理由.

-
科目: 来源: 题型:
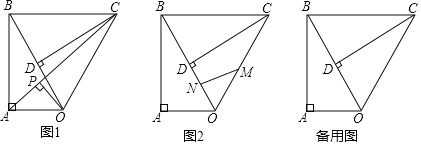
查看答案和解析>>【题目】已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O顺时针旋转60°,如题图1,连接BC.
(1)填空:∠OBC= °;
(2)如图1,连接AC,作OP⊥AC,垂足为P,求OP的长度;
(3)如图2,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒,设运动时间为x秒,△OMN的面积为y,求当x为何值时y取得最大值?最大值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“美丽沧州,清洁乡村”活动中,高家村村长提出了两种购买垃圾桶方案;方案1:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用250元;方案2:买不分类垃圾桶,需要费用1000元,以后每月的垃圾处理费用500元;设方案1的购买费用和每月垃圾处理费用共为
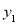 元,交费时间为x个月;方案2的购买费和每月垃圾处理费共为
元,交费时间为x个月;方案2的购买费和每月垃圾处理费共为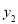 元,交费时间为x个月.
元,交费时间为x个月.(1)直接写出
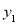 、
、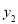 与x的函数关系式;
与x的函数关系式;(2)在同一坐标系内,画出两个函数的图像;
(3)在垃圾桶使用寿命相同的情况下,哪种方案省钱?
相关试题

