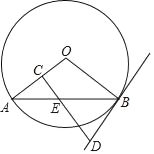
【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)由切线性质及等量代换推出∠4=∠5,再利用等角对等边可得出结论;
(2)由已知条件得出sin∠DEF和sin∠AOE的值,利用对应角的三角函数值相等推出结论.
试题解析:(1)∵DC⊥OA, ∴∠1+∠3=90°, ∵BD为切线,∴OB⊥BD, ∴∠2+∠5=90°, ∵OA=OB, ∴∠1=∠2,∵∠3=∠4,∴∠4=∠5,在△DEB中, ∠4=∠5,∴DE=DB.
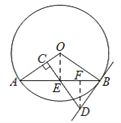
(2)作DF⊥AB于F,连接OE,∵DB=DE, ∴EF=![]() BE=3,在 RT△DEF中,EF=3,DE=BD=5,EF=3 , ∴DF=
BE=3,在 RT△DEF中,EF=3,DE=BD=5,EF=3 , ∴DF=![]() ∴sin∠DEF=
∴sin∠DEF=![]() =
= ![]() , ∵∠AOE=∠DEF, ∴在RT△AOE中,sin∠AOE=
, ∵∠AOE=∠DEF, ∴在RT△AOE中,sin∠AOE=![]() ,
,
∵AE=6, ∴AO=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点O在直线PQ上,过点O作射线OC,使∠POC=130°,将一直角三角板的直角顶点放在点O处.
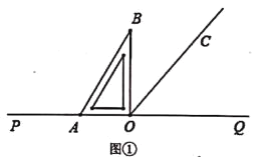
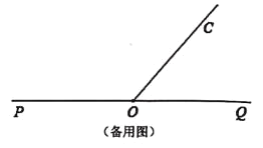
(1)如图①所示,将直角三角板AOB的一边OA与射线OP重合,则∠BOC=________°.
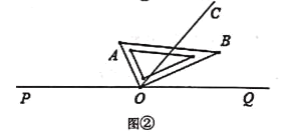
(2)将图①中的直角三角板AOB绕点O旋转一定角度得到如图②所示的位置,若OA平分∠POC,求∠BOQ的度数.
(3)将图①中的直角三角板AOB绕点O旋转一周,存在某一时刻恰有OB⊥OC,求出所有满足条件的∠AOQ的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图:反比例函数y=
 的图象经过点A(﹣3,b)过点A作x轴的垂线,垂足为B,S△AOB=3.
的图象经过点A(﹣3,b)过点A作x轴的垂线,垂足为B,S△AOB=3.(1)求k,b的值;
(2)若一次函数y=ax+1的图象经过点A,且与x轴交于M,求AM的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】为拓宽销售渠道,某水果商店计划将146个柚子和400个橙子装入大、小两种礼箱进行出售,其中每件小礼箱装2个柚子和4个橙子;每件大礼箱装3个柚子和9个橙子.要求每件礼箱都装满,柚子恰好全部装完,橙子有剩余,设小礼箱的数量为x件.
(1)大礼箱的数量为________件(用含x的代数式表示).
(2)若橙子剩余12个,则需要大、小两种礼箱共多少件?
(3)由于橙子有剩余,则小礼箱至少需要________件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从左至右第1个图由1个正六边形,6个正方形和6个等边三角形组成;第二个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成按此规律,第
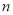 个图中正方形和等边三角形的个数之和为( )
个图中正方形和等边三角形的个数之和为( )
A.
 个B.
个B.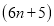 个C.
个C.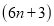 个D.
个D.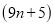 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的动点,P是线段BD上的一个动点,则PM+PN的最小值是( )

A.
 B.
B. 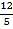 C.
C. 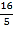 D.
D. 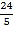
相关试题

