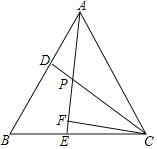
【题目】等边三角形ABC中,D、E分别是AB、BC上的点,且AD=BE,AE、CD相交于点P,CF⊥AE.
(1)求∠CPE的度数;
(2)求证:PF=![]() PC.
PC.
参考答案:
【答案】(1)∠CPE=60°;(2)见详解.
【解析】
(1)先根据已知条件判定出△BEA≌△CAD,得到CD=AE,再结合已知可证△CDB≌△ACE,由此可得∠AEC十∠CPE+∠PCE=∠BDC+∠PCE+∠B,即可知∠B=∠CPE=60°;
(2)由CF⊥AE,∠CPE=60°,可得△CPF是含30°角的直角三角形,即可证明.
(1)∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠B,
又∵AD=BE,
∴△BEA≌△CAD,BD=CE,
∴CD=AE,
又∵∠ACB=∠B,
∴△CDB≌△ACE,
∴∠BDC=∠AEC,
∴∠AEC十∠CPE+∠PCE=∠BDC+∠PCE+∠B,
∴∠B=∠CPE=60°;
(2)∵CF⊥AE,∠CPE=60°,
∴∠FCP=30°,
∴PF=![]() PC.
PC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E分别在边AB、AC上,DE、BC的延长线相交于点F,且
 .
.(1)求证
 ;
;(2)当AB=12,AC=9,AE=8时,求BD的长与
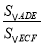 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线与x轴相交于点A(-2,0)、B(4,0),与y轴交于点C(0,-4),BC与抛物线的对称轴相交于点D.
(1)求该抛物线的表达式,并直接写出点D的坐标;
(2)过点A作AE⊥AC交抛物线于点E,求点E的坐标;
(3)在(2)的条件下,点F在射线AE上,若△ADF∽△ABC,求点F 的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】水池有若干个进水口与出水口,每个口进出水的速度如图1、图2所示,只开1个进水口持续15小时可将水池注满.

(1)某段时间内蓄水量V(m3)与时间t(h)的关系如图3所示,0~3时只开2个进水口,3~b时只开1个进水口与1个出水口,9~c只开1个出水口,求证:a=b+c.
(2)若同时开2个出水口与1个进水口,多久可将满池的水排完?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB=5,AD=4,AD∥BM,
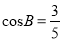 (如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x,
(如图),点C、E分别为射线BM上的动点(点C、E都不与点B重合),联结AC、AE,使得∠DAE=∠BAC,射线EA交射线CD于点F.设BC=x,  .
.(1)如图1,当x=4时,求AF的长;
(2)当点E在点C的右侧时,求y关于x的函数关系式,并写出函数的定义域;
(3)联结BD交AE于点P,若△ADP是等腰三角形,直接写出x的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)求证:三角形三个内角的和等于180°.
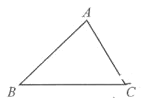
(2)阅读材料并回答问题:
如图,把△ABC的一边BC延长,得到∠ACD.像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的“外角”,在每个顶点处取这个三角形的一个外角,它们的和叫做这个三角形的“外角和”.补全图形并求△ABC的“外角和”.
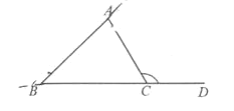
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p.
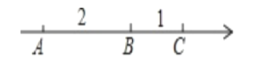
(1)若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少?
(2)若原点O在图中数轴上点C的右边,且CO=28,求p.
相关试题

