Question

【题目】探究并解决问题：

探究

倍延三角形的一条中线，我们可以发现一些有用的结论.

已知，如图①所示，AD为△ABC的中线，延长AD到E,使AD=DE,连接BE、CE.

（1）求证：AB∥CE.

（2）请再写出两条不同类型的结论.

解决问题

如图所示②，分别以△ABC的边AB和AC为边，向三角形的外侧作两个等腰直角三角形，AB=AD,AC=AE,∠BAD = ∠CAE=90°，点M为BC的中点，连接DE,AM,试问线段AM、DE之间存在什么关系？并说明理由.

Answer 1

【答案】探究（1）见解析；（2）见解析；解决问题：ED=2AM，AM⊥ED；证明见解析.

【解析】

探究（1）先证明四边形BEAC是平行四边形，即可完成；（2）根据（1）所得的平行四边形，写两条性质即可；解决问题：ED=2AM，AM⊥ED.延长AM到G，使MG=AM，连BG，则ABGC是平行四边形，再结合已知条件可以证明△DAE≌△ABG，根据全等三角形的性质可以得到DE=2AM，∠BAG=∠EDA，再延长MG交DE于H，因为∠B4G+∠DAH=90°，所以∠HDA+∠DAH=90°这样就证明了AMLED；

解：探究（1）∵AD为△ABC的中线，

∴BD=DC

又∵AD=DE

∴四边形ABEC是平行四边形

∴AB∥CE

（2）∵四边形ABEC是平行四边形

∴BE=AC,BE∥AC，∠BAC=∠BEC等写两个即可.

解决问题：

ED=2AM，AM⊥ED

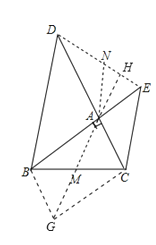
证明：延长AM到G，使MG=AM，连BG，则ABGC是平行四边形，再延长M4交DE于H.

∴AC=BG，∠ABG+∠BAC=180°

又∵∠DAE+∠BAC=180°，

∴∠ABG=∠DAE.

∴△DAE≌△ABG

∴DE=2AM，∠BAG=∠EDA.

延长MA交DE于H，

∵∠BAG+∠DAH=90°，

∴∠HDA+∠DAH=90°.

AM⊥ED.