【题目】叙述并证明三角形内角和定理.
三角形内角和定理: ;
已知:如图△ABC.
求证: .
证明:

参考答案:
【答案】三角形的内角和是180°;∠A+∠B+∠C=180°;证明见解析.
【解析】
要证明三角形的三个内角的和为180°,可以把三角形三个角转移到一个平角上,利用平角的性质解答.
解:定理:三角形的内角和是180°;
已知:如图△ABC;
求证:∠A+∠B+∠C=180°.
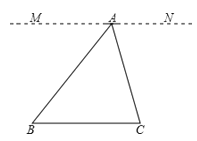
证明:过点作直线MN,使MN//BC.
∵MN∥BC,
∴∠B=∠MAB,∠C=∠NAC(两直线平行,内错角相等)
又∵∠MAB+∠NAC+∠BAC=180°(平角定义)
∴∠B+∠C+∠BAC=180°(等量代换)即∠A+∠B+∠C=180°.
故答案为:三角形的内角和是180°;∠A+∠B+∠C=180°;证明见解析.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,
 ,
, ,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小;
(3)求CQ的长.

-
科目: 来源: 题型:
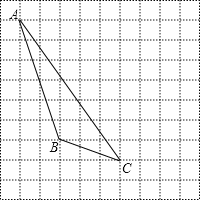
查看答案和解析>>【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
(1)画出△ABC的AB边上的中线CD;
(2)画出△ABC向右平移4个单位后得到的△A1B1C1;
(3)图中AC与A1C1的关系是: ;
(4)能使S △ABQ=S △ABC的格点Q,共有 个,在图中分别用Q 1,Q 2,…表示出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )

A. 1<m<11 B. 2<m<22 C. 10<m<12 D. 5<m<6
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进A、B两种商品,若购进A种商品2件和B种商品1件需45元;若购进A种商品3件和B种商品2件需70元.
(1)A、B两种商品每件的进价分别是多少元?
(2)若购进A、B两种商品共100件,总费用不超过1000元,最多能购进A种商品多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠C=90°,AB=8,AD=CD=5,点M为BC上异于B、C的一定点,点N为AB上的一动点,E、F分别为DM、MN的中点,当N从A到B的运动过程中,线段EF扫过图形的面积为 ( )

A.4B.4.5C.5D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究并解决问题:
探究
倍延三角形的一条中线,我们可以发现一些有用的结论.
已知,如图①所示,AD为△ABC的中线,延长AD到E,使AD=DE,连接BE、CE.
(1)求证:AB∥CE.

(2)请再写出两条不同类型的结论.
解决问题
如图所示②,分别以△ABC的边AB和AC为边,向三角形的外侧作两个等腰直角三角形,AB=AD,AC=AE,∠BAD = ∠CAE=90°,点M为BC的中点,连接DE,AM,试问线段AM、DE之间存在什么关系?并说明理由.
相关试题

