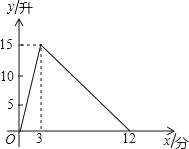
【题目】一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.
①当0≤x≤3时,求y与x之间的函数关系.
②3<x≤12时,求y与x之间的函数关系.
③当容器内的水量大于5升时,求时间x的取值范围.
参考答案:
【答案】①当0≤x≤3时,y与x之间的函数关系式为y=5x;
②![]() ;
;
③1<x<9.
【解析】
①当0≤x≤3时,设y=mx(m≠0),根据图象当x=3时,y=15求出m即可;
②当3<x≤12时,设y=kx+b(k≠0),根据图象过点(3,15)和点(12,0),然后代入求出k和b即可;
③根据函数图象的增减性求出x的取值范围即可.
解:①当0≤x≤3时,设y=mx(m≠0),
则3m=15,
解得m=5,
∴当0≤x≤3时,y与x之间的函数关系式为y=5x;
②当3<x≤12时,设y=kx+b(k≠0),
∵函数图象经过点(3,15),(12,0),
∴![]() ,解得:
,解得: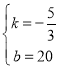 ,
,
∴当3<x≤12时,y与x之间的函数关系式y=﹣![]() x+20;
x+20;
③当y=5时,由5x=5得,x=1;
由﹣![]() x+20=5得,x=9.
x+20=5得,x=9.
∴由图象可知,当容器内的水量大于5升时,时间x的取值范围是1<x<9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(0,4)是直角坐标系y轴上一点,动点P从原点O出发,沿x轴正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.
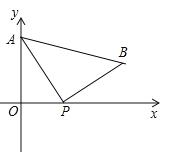
(1)若AB//x轴,求t的值;
(2)当t=3时,坐标平面内有一点M(不与A重合),使得以M、P、B为顶点的三角形和△ABP全等,请求出点M的坐标;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学举办“网络安全知识答题竞赛”,七、八年级根据初赛成绩各选出5名选手组成代表队参加决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分)
中位数(分)
众数(分)
方差(分2)
七年级
a
85
b
S七年级2
八年级
85
c
100
160
(1)根据图示填空:a= ,b= ,c= ;
(2)结合两队成绩的平均数和中位数进行分析,哪个代表队的决赛成绩较好?
(3)计算七年级代表队决赛成绩的方差S七年级2,并判断哪一个代表队选手成绩较为稳定.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A1、A2、A3、…、An在x轴上,且OA1=A1A2=A2A3=…=An﹣1An=1,分别过点A1、A2、A3、An作x轴的垂线,交反比例函数y=
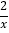 (x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2018=_____.
(x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2018=_____.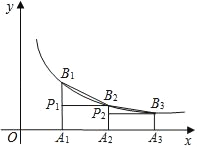
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形ABC中,AB=AC,点D是AC上一点。点E在BD的延长线上,且AB=AE,AF平分∠CAE交DE于点F,连接CF
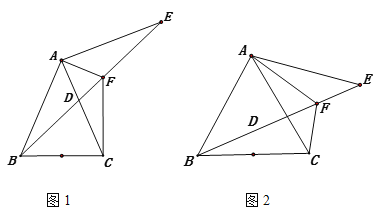
(1)如图1,找到与∠CFB相等的角,并证明
(2)如图2,如当∠ABC=60°,AF=m,EF=n时,求FB的长(用含m、n的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°.
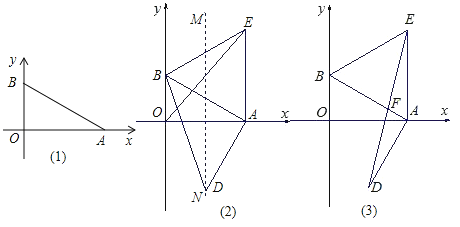
(1)求AB的长度;
(2)以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点,求证:BD=OE;
(3)在(2)的条件下,连接DE交AB于F,求证:F为DE的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富老年人的晚年生活,甲、乙两单位准备组织退休职工到某风景区游玩.甲、乙两单位退休职工共
 人,其中乙单位人数少于
人,其中乙单位人数少于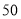 人,且甲单位人数不够
人,且甲单位人数不够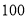 人.经了解,该风景区的门票价格如下表:
人.经了解,该风景区的门票价格如下表:数量(张)
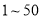

 张及以上
张及以上单价(元/张)
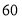
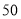

如果两单位分别单独购买门票,一共应付
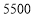 元.
元.(1)甲、乙两单位各有多少名退休职工准备参加游玩?
(2)如果甲单位有
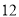 名退休职工因身体原因不能外出游玩,那么你有几种购买方案,通过比较,你该如何购买门票才能最省钱?
名退休职工因身体原因不能外出游玩,那么你有几种购买方案,通过比较,你该如何购买门票才能最省钱?
相关试题

