【题目】如图,A(0,4)是直角坐标系y轴上一点,动点P从原点O出发,沿x轴正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.
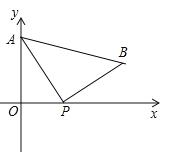
(1)若AB//x轴,求t的值;
(2)当t=3时,坐标平面内有一点M(不与A重合),使得以M、P、B为顶点的三角形和△ABP全等,请求出点M的坐标;
参考答案:
【答案】(1)4;(2) (4,7)或(10,-1)或(6,-4)或(0,4).
【解析】
(1)由AB∥x轴,可找出四边形ABCO为长方形,再根据△APB为等腰三角形可得知∠OAP=45°,从而得出△AOP为等腰直角三角形,由此得出结论;
(2)由全等三角形的性质和等腰三角形的性质可得出结论,注意分类讨论.
解:(1)过点B作BC⊥x轴于点C,如图所示.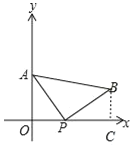
∵AO⊥x轴,BC⊥x轴,且AB∥x轴,
∴四边形ABCO为长方形,
∴AO=BC=4.
∵△APB为等腰直角三角形,
∴AP=BP,∠PAB=∠PBA=45°,
∴∠OAP=90°-∠PAB=45°,
∴△AOP为等腰直角三角形,
∴OA=OP=4.
∴t=4÷1=4(秒),
故t的值为4.
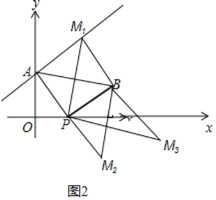
(2)当t=3时,OP=3.
∵OA=4,
∴由勾股定理,得
AP=![]() =5.
=5.
∴AP=PB=5,AB=5![]() ,
,
∴当△MPB≌△ABP时,此时四边形APBM1是正方形,四边形APBM3是平行四边形,易得M1(4,7)、M3(10,-1);
当△MPB≌△APB时,此时点M2与点A关于点P对称,易得M2(6,-4).
当两个三角形重合时,此时符合条件的点M的坐标是(0,4);
综上所述,点M的坐标为(4,7)或(10,-1)或(6,-4)或(0,4);
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭,小明家中买了一辆小轿车,他连续记录了
 天中每天行驶的路程(如下表),以
天中每天行驶的路程(如下表),以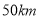 为标准,多于
为标准,多于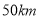 的记为“
的记为“ ”,不足
”,不足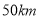 的记为“
的记为“ ”,刚好
”,刚好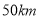 的记为“
的记为“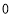 ”.
”.第一天
第二天
第三天
第四天
第五天
第六天
第七天
路程
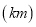

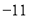

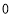
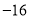

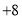
(1)请求出这
 天中平均每天行驶多少千米?
天中平均每天行驶多少千米?(2)若每行驶
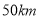 需用汽油
需用汽油 升,汽油价
升,汽油价 元/升,计算小明家这
元/升,计算小明家这 天的汽油费用大约是多少元?
天的汽油费用大约是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
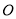 为直线
为直线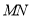 上的一点,且
上的一点,且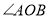 为直角,
为直角,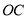 平分
平分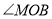 .
.(1)如图1,若
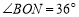 ,则
,则 等于多少度;
等于多少度;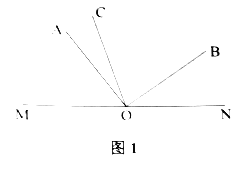
(2)如图2,若
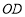 平分
平分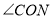 ,且
,且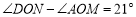 ,求
,求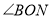 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2013年浙江义乌12分)如图1,已知
 (x>
(x>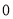 )图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连结AQ,取AQ的中点为C.
)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连结AQ,取AQ的中点为C.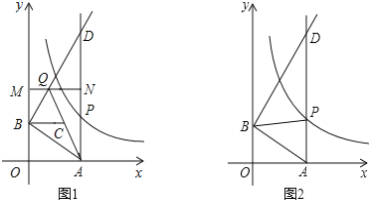
(1)如图2,连结BP,求△PAB的面积;
(2)当点Q在线段BD上时,若四边形BQNC是菱形,面积为
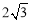 ,求此时P点的坐标;
,求此时P点的坐标;(3)当点Q在射线BD上时,且a=3,b=1,若以点B,C,N,Q为顶点的四边形是平行四边形,求这个平行四边形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学举办“网络安全知识答题竞赛”,七、八年级根据初赛成绩各选出5名选手组成代表队参加决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分)
中位数(分)
众数(分)
方差(分2)
七年级
a
85
b
S七年级2
八年级
85
c
100
160
(1)根据图示填空:a= ,b= ,c= ;
(2)结合两队成绩的平均数和中位数进行分析,哪个代表队的决赛成绩较好?
(3)计算七年级代表队决赛成绩的方差S七年级2,并判断哪一个代表队选手成绩较为稳定.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A1、A2、A3、…、An在x轴上,且OA1=A1A2=A2A3=…=An﹣1An=1,分别过点A1、A2、A3、An作x轴的垂线,交反比例函数y=
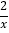 (x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2018=_____.
(x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2018=_____.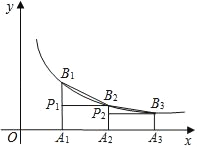
-
科目: 来源: 题型:
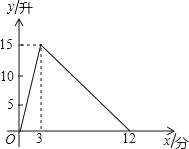
查看答案和解析>>【题目】一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.
①当0≤x≤3时,求y与x之间的函数关系.
②3<x≤12时,求y与x之间的函数关系.
③当容器内的水量大于5升时,求时间x的取值范围.
相关试题

